Consider the two general stochastic processes x1 = (x1t) and x2 = (x2t) defined by the dynamics

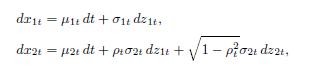
where z1 and z2 are independent one-dimensional standard Brownian motions. Interpret μit, it, and t.
Define the processes y = (yt) and w = (wt) by yt = x1tx2t and wt = x1t/x2t. What is the dynamics of y and w? Concretize your answer for the special case where x1 and x2 are geometric Brownian motions with constant correlation, i.e. μit = μixit, it = ixit, and t = with μi, i, and being constants.

Transcribed Image Text:

drit = dt + 01+ dzi dr =2 dt + pr2 dz + 1-p02 dz2t,