EXERCISE 5.4 Constantinides (1992) develops a theory of the nominal term structure of interest rates by specifying exogenously the nominal state-price deflator ˜. In a slightly simplified version, his assumption is that

where g and are constants, and x = (xt) follows the Ornstein-Uhlenbeck process dxt = −xt dt + dzt, where and are positive constants with 2 and z = (zt) is a standard one-dimensional Brownian motion.

(a) Derive the dynamics of the nominal state-price deflator. Express the nominal short-term interest rate, ˜rt, and the nominal market price of risk, ˜t, in terms of the variable xt.

(b) Find the dynamics of the nominal short rate.

(c) Find parameter constrains that ensure that the short rate stays positive? Hint: The short rate is a quadratic function of x. Find the minimum value of this function.

(d) What is the distribution of xT given xt?

(e) Let Y be a normally distributed random variable with mean μ and variance v2. Show that

(f) Use the results of the two previous questions to derive the time t price of a nominal zero-coupon bond with maturity T, i.e. ˜B T t . It will be an exponential-quadratic function of xt. What is the yield on this bond?
(g) Find the percentage volatility T t of the price of the zero-coupon bond maturing at T.
(h) The instantaneous expected excess rate of return on the zero-coupon bond maturing at T is often called the term premium for maturity T. Explain why the term premium is given by T t ˜
t and show that the term premium can be written as

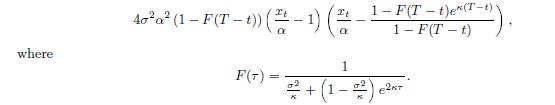
For which values of xt will the term premium for maturity T be positiveegative? For a given state xt, is it possible that the the term premium is positive for some maturities and negative for others?