(a) Show that the dispersion relation for the longitudinal plasma wave (with k = kx̂), for the case of an unbounded homogeneous plasma in which the motion of the electrons and the ions is taken into account, can be written as

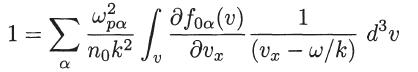
where α = e, i. Show that this dispersion relation can be recast into the form

where (with α = e, i)

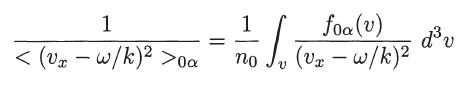
(b) For the cold plasma model, for which

show that the dispersion relation reduces to

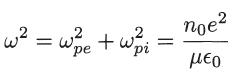
where μ = m_em_i(m_e + m_i) is the reduced mass of an electron and an ion.

(c) In the high phase velocity limit, show, by making a binomial expansion, that the dispersion relation becomes

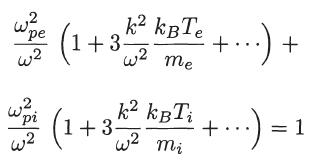
Show that this equation can be written as

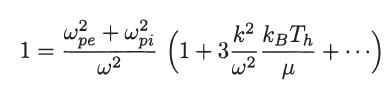
where T_h is a hybrid temperature given by

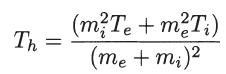
Under what conditions does this relation reduce to the Bohm-Gross dispersion relation for a warm electron plasma?

(d) Show that the dispersion relation of part (a) can be expressed as

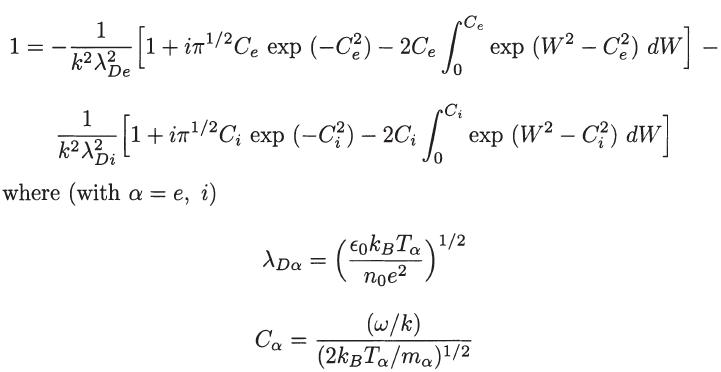
For weakly damped oscillations (ω_i ≪ ω_r) and in the low-frequency and low phase velocity range specified by the condition

show that the dispersion relation reduces to

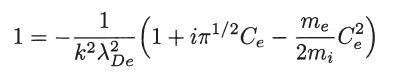
Consequently, verify that the frequency of oscillation and the Landau damping constant are given by

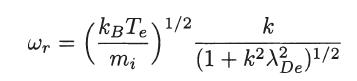
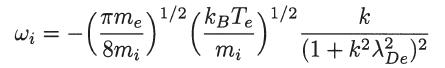
Note that the condition C_i ≫ 1 ≫ C_e is fulfilled only if T_e/T_i ≫ (1 + k²λ²_De), which implies a strongly non-isothermal plasma, with hot electrons and cold ions. Show that in the long-wave range we find

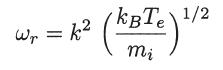
which is essentially the same as the low-frequency ion acoustic waves that propagate at a sound speed determined by the ion mass and the electron temperature.

Transcribed Image Text:

1 = Σ α w? ρα nok2 ofoa(v) 1 δυα (υα - w/k) Το υ dv