Since the longitudinal plasma wave is an electrostatic oscillation, it is possible to derive its dispersion relation
Question:
Since the longitudinal plasma wave is an electrostatic oscillation, it is possible to derive its dispersion relation using Poisson equation, satisfied by the electrostatic potential ϕ( r, t), instead of Maxwell equations. Consider the problem of small-amplitude longitudinal waves propagating in the x direction in an electron gas (only electrons move in a background of stationary ions), in the absence of a magnetic field. Assume that
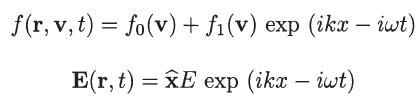
where |f1| ≪ f0 , with f0(v) the nonperturbed equilibrium distribution function and where E(r, t) is the internal electric field due to the small namplitude perturbation in the electron gas. Using the linearized Vlasov equation (neglecting second-order terms) determine the expression for f1(v) in terms of E = –∇ϕ and ∇vf0. Using this result in Poisson equation, obtain the following dispersion relation for longitudinal waves propagating in the x direction
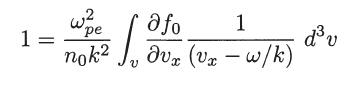
Step by Step Answer:






