Another type of wave mode that can be found from a fluid description of a plasma (but requires a kinetic treatment to understand completely) is a drift wave. Just as the two-stream instability provides a mechanism for plasmas to erase nonuniformity in velocity space, so drift waves can rapidly remove spatial irregularities.

The limiting case that we consider here is a modification of an ion-acoustic mode in a strongly magnetized plasma with a density gradient. Suppose that the magnetic field is uniform and points in the e_z direction. Let there be a gradient in the equilibrium density of both the electrons and the protons: n₀ = n₀(x). In the spirit of our description of ion-acoustic modes in an unmagnetized, homogeneous plasma [cf. Eq. (21.33)], treat the proton fluid as cold, but allow the electrons to be warm and isothermal with temperature T_e. We seek modes of frequency ω propagating perpendicular to the density gradient [i.e., with k = (0, k_y , k_z)].

(a) Consider the equilibrium of the warm electron fluid, and show that there must be a fluid drift velocity along the direction e_y of magnitude

where V_ia = (k_BT_e/m_p)^1/2 is the ion-acoustic speed. Explain in physical terms the origin of this drift and why we can ignore the equilibrium drift motion for the ions (protons).

(b) We limit our attention to low-frequency electrostatic modes that have phase velocities below the Alfvén speed. Under these circumstances, perturbations to the magnetic field can be ignored, and the electric field can be written as E = −∇Φ.Write down the three components of the linearized proton equation of motion in terms of the perturbation to the proton density n, the proton fluid velocity u, and the electrostatic potential Φ.

(c) Write down the linearized equation of proton continuity, including the gradient in n₀, and combine with the equation of motion to obtain an equation for the fractional proton density perturbation at low frequencies:

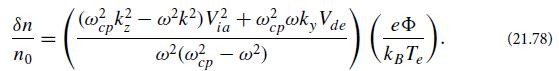
(d) Argue that the fractional electron-density perturbation follows a linearized Boltzmann distribution, so that

(e) Use both the proton- and the electron-density perturbations in Poisson’s equation to obtain the electrostatic drift wave dispersion relation in the low-frequency (ω ≪ ω_cp), long-wavelength (kλ_D ≪ 1) limit

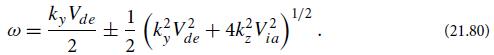
Describe the physical character of the mode in the additional limit k_z →0. A proper justification of this procedure requires a kinetic treatment, which also shows that, under some circumstances, drift waves can be unstable and grow
exponentially.

Equations 21.33.

Transcribed Image Text:

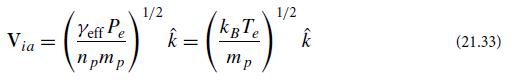
Vde V², 1 dno @ci no dx (21.77)