Consider a rocket once it is beyond the Earth's gravitational field.
Let:
v = constant velocity of the exhaust gas relative to the rocket.
u(t) = instantaneous velocity of the rocket.
M(t) = instantaneous total mass of the rocket.
–dM/dt =constant time rate of decrease of M(t), that is, the mass expelled per unit time.

(a) Verify that the equation of motion (Newton's second law) for the rocket is

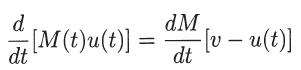
and show that the instantaneous acceleration of the rocket is

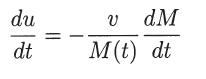
(b) Integrate the equation of motion to show that

(c) If the rocket burns for a time interval δt = t – t_o and if M (t) « M (t_o), show that the initial acceleration of the rocket is

(d) Calculate numerically (du/dt)_to and u(t) for a chemical rocket with v = 10³ m/s and δt = 10 s; and also for a plasma propulsion system with v = 10⁴ m/s and δt = 100 days. For the calculation of u(t) consider u(t_o) = 0 and M(t_o) = 10 M(t).

Transcribed Image Text:

d dt [M(t)u(t)] = = dM dt [v-u(t)]