In the expression deduced for ef in part (b) of the previous problem (high-frequency limit), consider

In the expression deduced for ν_ef in part (b) of the previous problem (high-frequency limit), consider that f₀ is the Maxwell-Boltzmann distribution function and that ν_r(v) = ν₀vⁿ, where ν₀ is a constant and n is an integer.

(a) Show that in this case we have

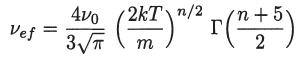
where Γ(z) is the gamma function defined by

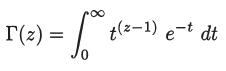
(b) Calculate the average value of the collision frequency < ν_r(v) >₀ , using the Maxwell-Boltzmann distribution function and show that

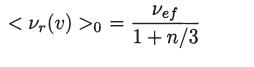
Data from Problem 5 part b.

Show that in the high-frequency limit (ω ≫ ν_ef) we have

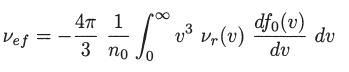
Thus, in both limits ν_ef is independent of ω.

Transcribed Image Text:

Vef (2kTn/2 = AV (2KT) n/² r(+5) 3√√π