Let (X,Y ) be randomvariablestakingvaluesin R+ N0 with a distributiondeterminedasfollows: X is drawnfromanexponentialdistributionwith mean yielding

Let (X,Y ) be randomvariablestakingvaluesin R+ × N0 with a distributiondeterminedasfollows: X is drawnfromanexponentialdistributionwith mean λ yielding thevalue x, andsubsequently Y is drawnfromaPoissondistribution with mean λx. Inotherwords,thejointdistributionof (X,Y ) has density

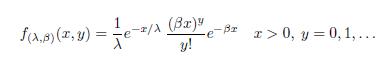
with respectto ν × m, where ν is thestandardLebesguemeasureon R+ and m is counting measureon N0.

a) Arguethatthefamilyofdistributionswithunknown (λ, β) ∈ R2 +, mayberep-
resented asaminimalandregulartwo-dimensionalexponentialfamily,determine the canonicalparameters,thecanonicalparameterspace,andassociatedcanon-
ical statistics,andcumulantfunction.

b) Findthemeanandcovariancematrixfor (X,Y )⊤.

c) Showthatthesubfamilygivenbytherestriction λ = β is acurvedexponential familyofdimensiononeandordertwo.

d) Findthelog-likelihoodfunction,scorefunction,Fisherinformation,andquad-
ratic scorefor β in thissubfamily.

Transcribed Image Text:

f(x,8)(x,y) = e2/A (Bx) y! Br x>0, y = 0,1,...