The following data represent the height (inches) of boys between the ages of 2 and 10 years.

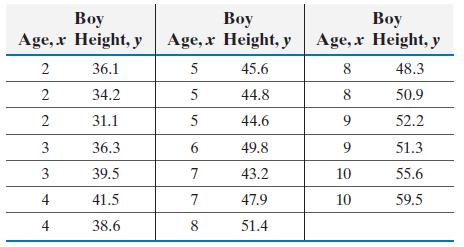
(a) Treating age as the explanatory variable, determine the estimates of ß₀ and ß₁. What is the mean height of a 7-year-old boy?
(b) Compute the standard error of the estimate, s_e.
(c) Assuming the residuals are normally distributed, test whether a linear relation exists between the explanatory variable, age, and response variable, height, at the α = 0.05 level of significance.
(d) Assuming the residuals are normally distributed, construct a 95% confidence interval for the slope of the true least-squares regression line.
(e) Construct a 90% confidence interval for the mean height found in part (a).
(f) Predict the height of a 7-year-old boy.
(g) Construct a 90% prediction interval for the height found in part (f).
(h) Explain why the predicted heights found in parts (a) and (f) are the same, yet the intervals are different.

Transcribed Image Text:

Boy Boy Boy Age, x Height, y Age, x Height, y Age, x Height, y 2 36.1 5 45.6 48.3 2 34.2 5 44.8 50.9 2 31.1 5 44.6 52.2 3 36.3 6 49.8 51.3 39.5 7 43.2 55.6 41.5 7 47.9 59.5 38.6 8 51.4 نیا 3 نیا 4 4 8 8 9 9 10 10