Assume that instead of a uniform distribution, in this market, the quality of cars X follows a

Question:

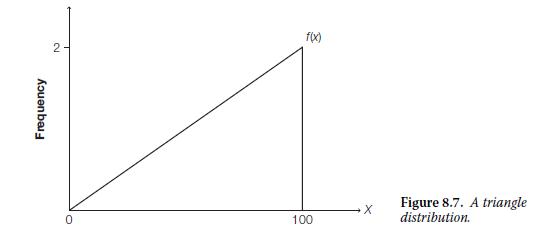
Assume that instead of a uniform distribution, in this market, the quality of cars X follows a triangle distribution from 0 to 100 as depicted in Figure 8.7.

Given this new distribution, the formula for expected value of X conditional on an upper bound P is E[X|22(P)]= -P (8.17)

Frequency 2 0 f(x) 100 Figure 8.7. A triangle distribution.

We assume the original seller and buyer utility specifications: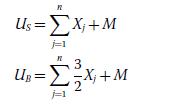 n Us = X + M 3 up =;x+ M 1

a. First assume P = $50. Will any cars sell in this market?

b. What is the range of prices for which cars will sell?

c. Describe in qualitative terms how the triangle distribution is different from the uniform distribution we assumed earlier. Do the sellers possess more high-quality cars or low-quality cars? How does this allow the market to function even in the face of asymmetric information?

d. Use the formula for conditional expectation below to derive equation (8.17). Note that f (x) is the probability density function and F_X(x) is the cumulative distribution function for the triangle distribution above. E[X|S2(P)]= xf (x) -dx Fx(P)

e. Now assume a different triangle distribution for car quality X as depicted in Figure 8.8. Without doing any calculations, predict whether the market will unravel. Justify your answer.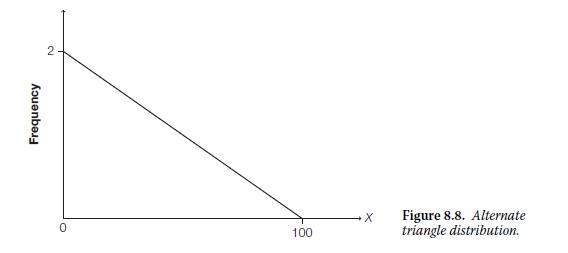 Frequency N 0 100 X Figure 8.8. Alternate triangle distribution.