As discussed in Example equation (1.28, zero-order kinetics is a good approximation to the Michaelis-Menten model if \(p_{A}\) is much larger than \(p_{0}\). However, when \(p_{A}\) and \(p_{0}\) are of the same order of magnitude, the complete Michaelis-Menten equation must be used to describe the reaction kinetics. In that case, 1-126) must be solved numerically.

(a) Show that equations (1-126) and (1-127) can be written in dimensionless form as

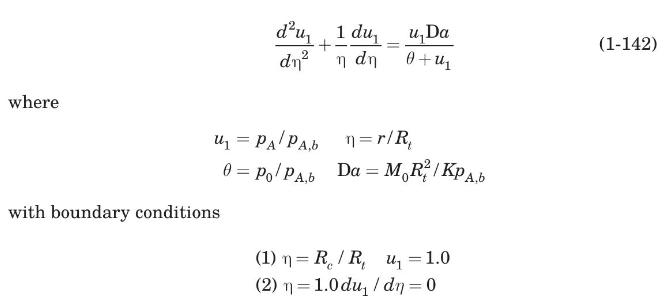
(b) Transform the second-order differential equation (1-142) into a system of two simultaneous first-order equations by defining \(u_{2}=d u_{1} / \mathrm{d} \eta\). The resulting boundary-value problem can be solved numerically by the shooting method using the rkfixed intrinsic function of Mathcad as illustrated in Example 1.17.
(c) For the conditions of Example equation (1.28, McGuire and Secomb (2001) showed that at the venous end of the capillary the oxygen partial pressure in blood had dropped to 25 torr. Solve 1-142) numerically and show that for these conditions, hypoxic conditions prevail all the way from a radial position of \(20 \mu \mathrm{m}\) to the end of the tissue cylinder at \(26 \mu \mathrm{M}\).

Data From Equation 1-28:-

Data From Equation 1-126 and 1-127:-

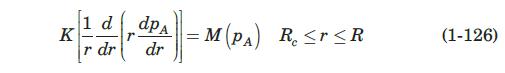
Data From Example 1.17:-

The Stefan tube, depicted schematically in Figure 1.8, is a simple device sometimes used for measuring diffusion coefficients in binary vapor mixtures. In the bottom of the tube is a pool of quiescent liquid. The vapor that evaporates from this pool

mole fraction of the diffusing vapors there to essentially zero. The composition of the vapor at the vapor–liquid interface is its equilibrium value. Carty and Schrodt (1975) evaporated a binary liquid mixture of acetone (1) and methanol (2) in a Stefan tube. Air (3) was used as the carrier gas. In one of their experiments the composition of the vapor at the liquid interface was y₁ = 0.319, y₂ = 0.528, and y₃ = 0.153. The pressure and temperature in the gas phase were 99.4 kPa and 328.5 K, respectively. The length of the diffusion path was 0.238 m. The MS diffusion coefficients of the three binary pairs are

Calculate the molar fluxes of acetone and methanol, and the composition profiles predicted by the MS equations. Compare your results with the experimental data.

Transcribed Image Text:

where du 1 du dn + n dn = u, Da 0+21 u = PA PAb =r/R 0 Po PA,b Da = MOR/KPA.b with boundary conditions (1) R/Ru = 1.0 (2) n = 1.0du/dn=0 (1-142)