At a different point in the packed distillation column of Example 3.10, the methanol content of the bulk of the gas phase \(76.2 \mathrm{~mol} \%\); that of the bulk of the liquid phase is \(60 \mathrm{~mol} \%\). The temperature at that point in the tower is around \(343 \mathrm{~K}\). The packing characteristics and flow rates at that point are such that \(F_{G}=1.542 \mathrm{~mol} / \mathrm{m}^{2} \cdot \mathrm{s}\) and \(F_{L}=8.650 \mathrm{~mol} / \mathrm{m}^{2} \cdot \mathrm{s}\). Calculate the interfacial compositions and the local methanol flux. To calculate the latent heats of vaporization at the new temperature, modify the values given in Example 3.6 using Watson's method (Smith et al., 1996):

For water, \(T_{c}=647.1 \mathrm{~K}\); for methanol, \(T_{c}=512.6 \mathrm{~K}\).

Data From Example 3.10:-

A mixture of methanol (substance A, the more volatile) and water (substance B) is being distilled in a packed tower at constant pressure of 1 atm. At a point along the tower, the methanol content of the bulk of the gas phase is 36 mol%; that of the bulk of the liquid phase is 20 mol%. The temperature at that point in the tower is around 360 K. At that temperature, the molar latent heat of vaporization of methanol is λ_A = 33.3 MJ/kmol, and that of water is λB = 41.3 MJ/kmol. The and flow conditions at that point are such that F_G = 0.0017 kmol/m2·s, and F_L = 0.0149 kmol/m2·s. Estimate the local flux of methanol from the liquid to the gas phase. The VLE for this system is adequately described by the modified Raoult’s law, equation (3-2), using the Wilson equation to estimate the activity coefficients (Smith et al., 1996)

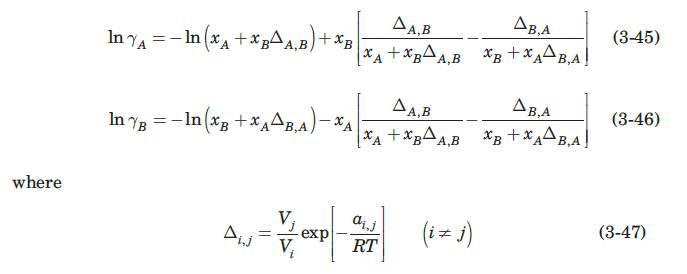
where V_j and V_i are the molar volumes at temperature T of pure liquids j and i and a_i,j is a constant independent of composition and temperature. Recommended values of the parameters for this system are V_A = 40.73 cm3/mol, VB = 18.07 cm3/mol, a_A,B = 107.38 cal/mol, a_B,A = 469.55 cal/mol (Smith et al., 1996).

Transcribed Image Text:

12 1-T2 11 1-T1 10.38 (3-86)