Consider a large plane wall of thickness L and constant thermal conductivity k. The left side of
Question:
Consider a large plane wall of thickness L and constant thermal conductivity k. The left side of the wall (x = 0) is maintained at a constant temperature T0, while the right surface at x = L is insulated. Heat is generated in the wall at the rate of ėgen = ax2 Btu/h · ft3. Assuming steady one-dimensional heat transfer,
(a) Express the differential equation and the boundary conditions for heat conduction through the wall,
(b) By solving the differential equation, obtain a relation for the variation of temperature in the wall T(x) in terms of x, L, k, a, and T0, and
(c) What is the highest temperature (ºC) in the plane wall when: L = 1 ft, k = 5 Btu/h · ft · ºF, a = 1200 Btu/h · ft5, and T0 = 700ºF.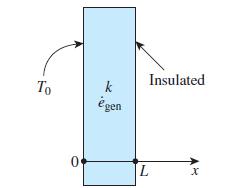
Step by Step Answer:

Heat And Mass Transfer Fundamentals And Applications
ISBN: 9780073398181
5th Edition
Authors: Yunus Cengel, Afshin Ghajar





