Consider Problem 4.62. An engineer desires to measure the surface temperature of the thin sheathing by painting it black \((\varepsilon=0.98)\) and using an infrared measurement device to nonintrusively determine the surface temperature distribution. Predict the temperature distribution of the painted surface, accounting for radiation heat transfer with large surroundings at \(T_{\text {sur }}=25^{\circ} \mathrm{C}\).

Data From Problem 4.62:-

A long, solid cylinder of diameter \(D=25 \mathrm{~mm}\) is formed of an insulating core that is covered with a very thin \((t=50 \mu \mathrm{m})\), highly polished metal sheathing of thermal conductivity \(k=25 \mathrm{~W} / \mathrm{m} \cdot \mathrm{K}\). Electric current flows through the stainless steel from one end of the cylinder to the other, inducing uniform volumetric heating within the sheathing of \(\dot{q}=5 \times 10^{6} \mathrm{~W} / \mathrm{m}^{3}\). As will become evident in Chapter 6, values of the convection

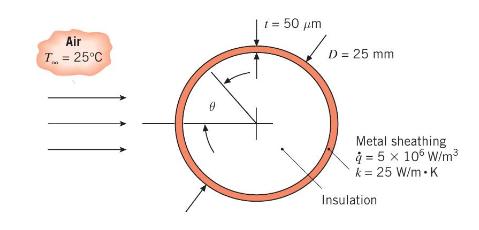coefficient between the surface and air for this situation are spatially nonuniform, and for the airstream conditions of the experiment, the convection heat transfer coefficient varies with the angle \(\theta\) as \(h(\theta)=\) \(26+0.637 \theta-8.92 \theta^{2}\) for \(0 \leq \theta

(a) Neglecting conduction in the \(\theta\)-direction within the stainless steel, plot the temperature distribution \(T(\theta)\) for \(0 \leq \theta \leq \pi\) for \(T_{\infty}=25^{\circ} \mathrm{C}\).

(b) Accounting for \(\theta\)-direction conduction in the stainless steel, determine temperatures in the stainless steel at increments of \(\Delta \theta=\pi / 20\) for \(0 \leq \theta \leq \pi\). Compare the temperature distribution with that of part (a).

Transcribed Image Text:

= 50 m Air T = 25C D = 25 mm Metal sheathing 4-5 x 106 W/m k = 25 W/m K Insulation