Consider Problem 8.38. A more realistic solution would account for the resistance to heat transfer due to free convection in the paraffin during melting. Assuming the tube surface to have a uniform temperature of \(55^{\circ} \mathrm{C}\) and the paraffin to be an infinite, quiescent liquid, determine the convection coefficient associated with the outer surface. Using this result and recognizing that the tube surface temperature is not known, determine the water outlet temperature, the total heat transfer rate, and the time required to completely liquefy the paraffin, for the prescribed conditions. Thermophysical properties associated with the liquid state of the paraffin are \(k=0.15 \mathrm{~W} / \mathrm{m} \cdot \mathrm{K}, \beta=8 \times 10^{-4} \mathrm{~K}^{-1}, ho=770 \mathrm{~kg} / \mathrm{m}^{3}\), \(v=5 \times 10^{-6} \mathrm{~m}^{2} / \mathrm{s}\), and \(\alpha=8.85 \times 10^{-8} \mathrm{~m}^{2} / \mathrm{s}\).

Data From Problem 8.38:-

Consider a horizontal, thin-walled circular tube of diameter \(D=0.025 \mathrm{~m}\) submerged in a container of \(n\)-octadecane (paraffin), which is used to store thermal energy. As hot water flows through the tube, heat is transferred to the paraffin, converting it from the solid to liquid state at the phase change temperature of \(T_{\infty}=27.4^{\circ} \mathrm{C}\). The latent heat of fusion and density of paraffin are \(h_{s f}=244 \mathrm{~kJ} / \mathrm{kg}\) and \(ho=770 \mathrm{~kg} / \mathrm{m}^{3}\), respectively, and thermophysical properties of the water may be taken as \(c_{p}=4.185 \mathrm{~kJ} / \mathrm{kg} \cdot \mathrm{K}, k=0.653 \mathrm{~W} / \mathrm{m} \cdot \mathrm{K}, \mu=\) \(467 \times 10^{-6} \mathrm{~kg} / \mathrm{s} \cdot \mathrm{m}\), and \(\operatorname{Pr}=2.99\). 

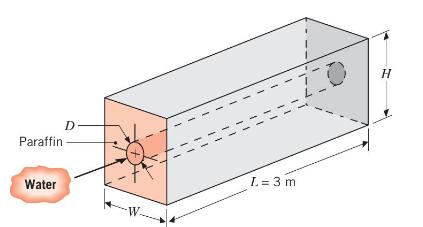
(a) Assuming the tube surface to have a uniform temperature corresponding to that of the phase change, determine the water outlet temperature and total heat transfer rate for a water flow rate of \(0.1 \mathrm{~kg} / \mathrm{s}\) and an inlet temperature of \(60^{\circ} \mathrm{C}\). If \(H=W=0.25 \mathrm{~m}\), how long would it take to completely liquefy the paraffin, from an initial state for which all the paraffin is solid and at \(27.4^{\circ} \mathrm{C}\) ?
(b) The liquefaction process can be accelerated by increasing the flow rate of the water. Compute and plot the heat rate and outlet temperature as a function of flow rate for \(0.1 \leq \dot{m} \leq 0.5 \mathrm{~kg} / \mathrm{s}\). How long would it take to melt the paraffin for \(\dot{m}=0.5 \mathrm{~kg} / \mathrm{s}\) ?

Transcribed Image Text:

Paraffin D Water W L= 3 m H