Consider the composite wall of Problem 3.11 under conditions for which the inside air is still characterized by \(T_{\infty, i}=20^{\circ} \mathrm{C}\) and \(h_{i}=30 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\). However, use the more realistic conditions for which the outside air is characterized by a diurnal (time) varying temperature of the form 

\[\begin{array}{ll}T_{\infty, o}(\mathrm{~K})=273+5 \sin \left(\frac{2 \pi}{24} t\right) & 0 \leq t \leq 12 \mathrm{~h} \\T_{\infty, o}(\mathrm{~K})=273+11 \sin \left(\frac{2 \pi}{24} t\right) & 12 \leq t \leq 24 \mathrm{~h}\end{array}\] with \(h_{o}=60 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\). Assuming quasi-steady conditions for which changes in energy storage within the wall may be neglected, estimate the daily heat loss through the wall if its total surface area is \(200 \mathrm{~m}^{2}\).

Data From Problem 3.11:-

A house has a composite wall of wood, fiberglass insulation, and plaster board, as indicated in the sketch. On a cold winter day, the convection heat transfer coefficients are \(h_{o}=60 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\) and \(h_{i}=30 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\). The total wall surface area is \(350 \mathrm{~m}^{2}\).

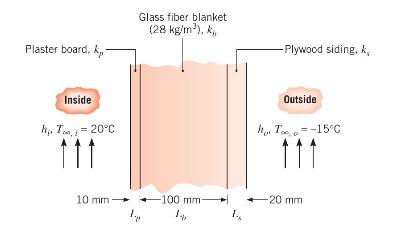
(a) Determine a symbolic expression for the total thermal resistance of the wall, including inside and outside convection effects for the prescribed conditions.

(b) Determine the total rate of heat loss through the wall.

(c) If the wind were blowing violently, raising \(h_{o}\) to \(300 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\), determine the percentage increase in the rate of heat loss.

(d) What is the controlling resistance that determines the amount of heat flow through the wall?

Transcribed Image Text:

Plaster board, k Glass fiber blanket (28 kg/m), k -Plywood siding, k Inside hi. Too = 20C 111 Outside Too-15C -20 mm 10 mm- 100 mm- 1-8