For the conditions described in Problem 1.39, determine the temperature distribution, \(T(r)\), in the container, expressing your result in terms of \(\dot{q}_{o}, r_{o}, T_{\infty}, h\), and the thermal conductivity \(k\) of the radioactive wastes.

Data From Problem 1.39:-

Radioactive wastes are packed in a long, thin-walled cylindrical container. The wastes generate thermal energy nonuniformly according to the relation \(\dot{q}=\dot{q}_{o}\left[1-\left(r / r_{\mathrm{o}}\right)^{2}\right]\), where \(\dot{q}\) is the local rate of energy generation per unit volume, \(\dot{q}_{o}\) is a constant, and \(r_{\mathrm{o}}\) is the radius of the container. Steady-state conditions are maintained by submerging the container in a liquid that is at \(T_{\infty}\) and provides a uniform convection coefficient \(h\).

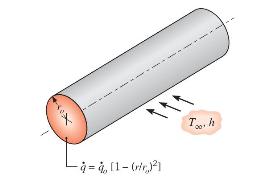
Obtain an expression for the total rate at which energy is generated in a unit length of the container. Use this result to obtain an expression for the temperature \(T_{s}\) of the container wall.

Transcribed Image Text:

-=[1-(r/r)] Th