Free convection heat transfer is sometimes quantified by writing Equation 4.20 as \(q_{\text {conv }}=S k_{\text {eff }} \Delta T_{1-2}\), where \(k_{\text {eff }}\) is an effective thermal conductivity. The ratio \(k_{\text {eff }} / k\) is greater than unity because of fluid motion driven by buoyancy forces, as represented by the dashed streamlines.

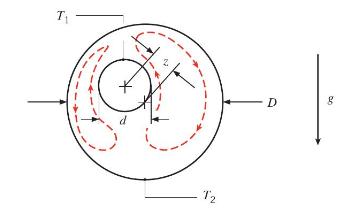An experiment for the configuration shown yields a heat transfer rate per unit length of \(q_{\text {conv }}^{\prime}=110 \mathrm{~W} / \mathrm{m}\) for surface temperatures of \(T_{1}=53^{\circ} \mathrm{C}\) and \(T_{2}=15^{\circ} \mathrm{C}\), respectively. For inner and outer cylinders of diameters \(d=20 \mathrm{~mm}\) and \(D=60 \mathrm{~mm}\), and an eccentricity factor of \(z=10 \mathrm{~mm}\), determine the value of \(k_{\text {eff. }}\). The actual thermal conductivity of the fluid is \(k=0.255 \mathrm{~W} / \mathrm{m} \cdot \mathrm{K}\).

Equation 4.20:-

Transcribed Image Text:

T g D d