In Section 5.5, the one-term approximation to the series solution for the temperature distribution was developed for a plane wall of thickness \(2 L\) that is initially at a uniform temperature and suddenly subjected to convection heat transfer. If \(B i

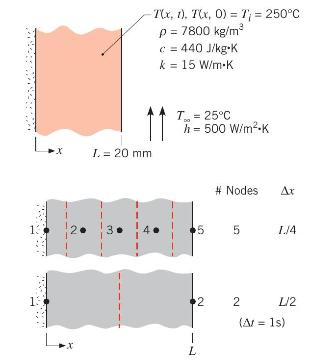
(a) Determine the midplane, \(T(0, t)\), and surface, \(T(L, t)\), temperatures at \(t=100,200\), and \(500 \mathrm{~s}\) using the one-term approximation to the series solution, Equation 5.43. What is the Biot number for the system?

(b) Treating the wall as a lumped capacitance, calculate the temperatures at \(t=50,100,200\), and \(500 \mathrm{~s}\). Did you expect these results to compare favorably with those from part (a)? Why are the temperatures considerably higher?

(c) Consider the 2- and 5-node networks shown schematically. Write the implicit form of the finitedifference equations for each network, and determine the temperature distributions for \(t=50,100,200\), and \(500 \mathrm{~s}\) using a time increment of \(\Delta t=1 \mathrm{~s}\). Prepare a table summarizing the results of parts (a), (b), and (c). Comment on the relative differences of the predicted temperatures.

Transcribed Image Text:

Tx, 1). T(x, 0) = T = 250C p = 7800 kg/m c = 440 J/kg K k = 15 W/m-K 11 T=25C h = 500 W/mK Lex I. = 20 mm 13 13 # Nodes Ax 5 5 1/4 2 2 L/2 (A = 1s) LX L