In studying the sublimation of naphthalene into an airstream, an investigator constructed a 3-m-long annular duct. The
Question:
In studying the sublimation of naphthalene into an airstream, an investigator constructed a 3-m-long annular duct. The inner pipe was made from a \(25-\mathrm{mm}-\mathrm{OD}\), solid naphthalene rod; this was surrounded by a 50-mm-ID naphthalene pipe. Air at \(289 \mathrm{~K}\) and \(1 \mathrm{~atm}\) flowed through the annular space at an average velocity of \(15 \mathrm{~m} / \mathrm{s}\). Estimate the partial pressure of naphthalene in the airstream exiting from the tube. At \(289 \mathrm{~K}\), naphthalene has a vapor pressure of \(5.2 \mathrm{~Pa}\), and a diffusivity in air of \(0.06 \mathrm{~cm}^{2} / \mathrm{s}\). Use the results of Problem 2.7 to estimate the mass-transfer coefficient for the inner surface and equation (2-74), using the equivalent diameter defined in Problem 2.7, to estimate the coefficient from the outer surface.
Data From Problem 2.7:-
(a) In studying rates of diffusion of naphthalene into air, an investigator replaced a \(30.5-\mathrm{cm}\) section of the inner pipe of an annulus with a naphthalene rod. The annulus was composed of a 51-mm-OD brass inner pipe that is surrounded by a 76-mm-ID brass pipe. While operating at a mass velocity within the annulus of \(12.2 \mathrm{~kg}\) of air \(/ \mathrm{m}^{2} \cdot \mathrm{s}\) at \(273 \mathrm{~K}\) and \(1 \mathrm{~atm}\), the investigator determined that the partial pressure of naphthalene in the exiting gas stream was \(0.041 \mathrm{~Pa}\). Under the conditions of the investigation, the Schmidt number of the gas was 2.57 , the viscosity was \(175 \mu \mathrm{P}\), and the vapor pressure of naphthalene was \(1.03 \mathrm{~Pa}\). Estimate the mass-transfer coefficient from the inner wall for this set of conditions. Assume that equation (2-87) applies.
(b) Monrad and Pelton (1942) presented the following correlation for the heattransfer coefficient in an annular space:
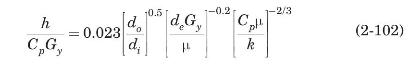
where \(d_{o}\) and \(d_{i}\) are the outside and inside diameters of the annulus, and \(d_{e}\) is the equivalent diameter defined as

Write down the analogous expression for mass transfer and use it to estimate the mass-transfer coefficient for the conditions of part (a). Compare the two results.
Equation 2-74:-
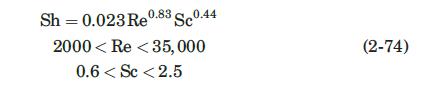
Step by Step Answer:






