The interfacial surface area per unit volume, \(a\), in many types of packing materials used in industrial towers is virtually impossible to measure. Both \(a\) and the mass-transfer coefficient depend on the physical geometry of the equipment and on the flow rates of the two contacting, immiscible streams. Accordingly, they are normally correlated together as the volumetric mass-transfer coefficient, \(k_{L} a\).
Empirical equations for the volumetric coefficients must be obtained experimentally for each type of mass-transfer operation. Sherwood and Holloway (1940) obtained the following correlation for the liquid-film mass-transfer coefficient in packed absorption towers:

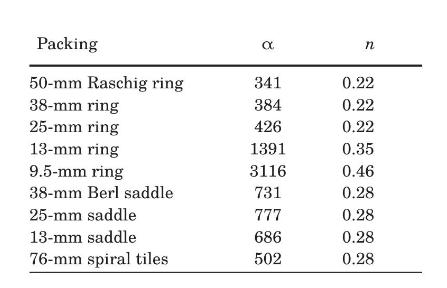
The values of \(\alpha\) and \(n\) to be used in equation (2-107) for various industrial packings are listed in the following table, when SI units are used exclusively.
(a) Consider the absorption of sulfur dioxide with water at \(294 \mathrm{~K}\) in a tower packed with \(25-\mathrm{mm}\) Raschig rings. If the liquid mass velocity is \(G_{x}=2.04 \mathrm{~kg} / \mathrm{m}^{2} \cdot \mathrm{s}\), estimate the liquid-film mass-transfer coefficient. The diffusivity of \(\mathrm{SO}_{2}\) in water is \(1.7 \times 10^{-9}\) \(\mathrm{m}^{2} / \mathrm{s}\) at \(294 \mathrm{~K}\).

(b) Whitney and Vivian (1949) measured rates of absorption of \(\mathrm{SO}_{2}\) in water and found the following expression for 25 -mm Raschig rings at \(294 \mathrm{~K}\)

where \(k_{x} a\) is in \(\mathrm{kmol} / \mathrm{m}^{3} \cdot \mathrm{s}\), and \(G_{x}\) is in \(\mathrm{kg} / \mathrm{m}^{2} \cdot \mathrm{s}\). For the conditions described in part (a), estimate the liquid-film mass-transfer coefficient using equation (2-108). Compare the results.

Transcribed Image Text:

ka DAB x pD AB 10.5 (2-107)