We consider a ternary tree (or trinomial) model with \(N+1\) time instants \(k=0,1, \ldots, N\) and \(d=1\) risky asset. The price \(S_{k}^{(0)}\) of the riskless asset evolves as

\[ S_{k}^{(0)}=S_{0}^{(0)}(1+r)^{k}, \quad k=0,1, \ldots, N \]

with \(r>-1\). Let the return of the risky asset \(S^{(1)}\) be defined as

\[ R_{k}:=\frac{S_{k}^{(1)}-S_{k-1}^{(1)}}{S_{k-1}^{(1)}}, \quad k=1,2, \ldots, N \]

In this ternary tree model, the return \(R_{k}\) is random and allowed to take only three values \

(a, 0\) and \(b\) at each time step, i.e.

\[ R_{k} \in\{a, 0, b\}, \quad k=1,2, \ldots, N \]

with \(-1S_{k}^{(1)}=\left\{\begin{array}{ll}
(1+b) S_{k-1}^{(1)} & \text { if } R_{k}=b \\
S_{k-1}^{(1)} & \text { if } R_{k}=0 \\
(1+a) S_{k-1}^{(1)} & \text { if } R_{k}=a \end{array}ight\}=\left(1+R_{k}ight) S_{k-1}^{(1)}, \quad k=1,2, \ldots, N \]
and \[
S_{k}^{(1)}=S_{0}^{(1)} \prod_{i=1}^{k}\left(1+R_{i}ight), \quad k=0,1, \ldots, N .
\]
The price process \(\left(S_{k}^{(1)}ight)_{k=0,1, \ldots, N}\) evolves on a ternary tree of the form:

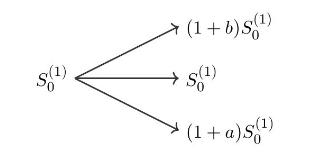
The information \(\mathcal{F}_{k}\) known to the market up to time \(k\) is given by the knowledge of \(S_{1}^{(1)}, S_{2}^{(1)}, \ldots, S_{k}^{(1)}\), i.e. we write \[
\mathcal{F}_{k}=\sigma\left(S_{1}^{(1)}, S_{2}^{(1)}, \ldots, S_{k}^{(1)}ight)=\sigma\left(R_{1}, R_{2}, \ldots, R_{k}ight)
\]
\(k=0,1, \ldots, N\), where, as a convention, \(S_{0}^{(1)}\) is a constant and \(\mathcal{F}_{0}=\{\emptyset, \Omega\}\) contains no information. In what follows we will consider that \(\left(R_{k}ight)_{k=1,2, \ldots, N}\) is a sequence of independent identically distributed random variables under any risk-neutral probability measure \(\mathbb{P}^{*}\), and we denote

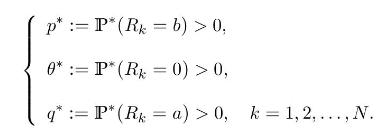
a) Determine all possible risk-neutral probability measures \(\mathbb{P}^{*}\) equivalent to \(\mathbb{P}\) in terms of the parameter \(\theta^{*} \in(0,1)\).

b) Give a necessary and sufficient condition for the absence of arbitrage in this ternary tree model.
Hint: Use your intuition of the market to find what the condition should be, and then prove that it is necessary and sufficient. Note that we have \(a0\), and the condition should only depend on the model parameters \

(a, b\) and \(r\).

c) When the model parameters allow for arbitrage opportunities, explain how you would exploit them if you joined the market with zero money to invest.

d) Is this ternary tree market model complete?

e) In this question we assume that the conditional variance \[
\operatorname{Var}^{*}\left[\left.\frac{S_{k+1}^{(1)}-S_{k}^{(1)}}{S_{k}^{(1)}} ightvert\, \mathcal{F}_{k}ight]=\sigma^{2}>0 \]
of the asset return \(\left(S_{k+1}^{(1)}-S_{k}^{(1)}ight) / S_{k}^{(1)}\) given \(\mathcal{F}_{k}\) is constant and equal to \(\sigma^{2}, k=\) \(0,1, \ldots, N-1\). Show that this condition determines a unique value of \(\theta^{*}\) and a unique risk-neutral probability measure \(\mathbb{P}_{\sigma}^{*}\) to be written explicitly, under a certain condition on \

(a,

b, r\) and \(\sigma\).

f) In this question and in the following we impose the condition \((1+a)(1+b)=1\), i.e. we let \(a:=-b /(b+1)\). What does this imply on this ternary tree model and on the risk-neutral probability measure \(\mathbb{P}^{*}\) ?
g) We consider a vanilla financial claim with payoff \(C=h\left(S_{N}ight)\) and maturity \(N\), priced as time \(k\) as \[
\begin{aligned}
f\left(k, S_{k}^{(1)}ight) & =\frac{1}{(1+r)^{N-k}} \mathbb{E}_{\theta}^{*}\left[h\left(S_{N}ight) \mid \mathcal{F}_{k}ight] \\
& =\frac{1}{(1+r)^{N-k}} \mathbb{E}_{\theta}^{*}\left[h\left(S_{N}ight) \mid S_{k}^{(1)}ight]
\end{aligned}
\]

\(k=0,1, \ldots, N\), under the risk-neutral probability measure \(\mathbb{P}_{\theta}^{*}\). Find a recurrence equation between the functions \(f(k, \cdot)\) and \(f(k+1, \cdot), k=0, \ldots, N-1\).
Hint: Use the tower property of conditional expectations.
h) Assuming that \(C\) is the payoff of the European put option with strike price \(K\), give the expression of \(f(N, x)\).
i) Modify the Python code below in order to make it deal with the trinomial model.
j) Taking \(S_{0}^{(1)}=1, r=0.1, b=1,(1+a)(1+b)=1\), compute the price at time \(k=0\) of the European put option with strike price \(K=1\) and maturity \(N=2\) using the code of Question (i) with \(\theta=0.5\).

Transcribed Image Text:

8(1) (1 + b)s() (1) (1 + a)s()