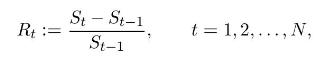We consider the discrete-time Cox-Ross-Rubinstein model with (N+1) time instants (t=0,1, ldots, N), with a riskless asset
Question:
We consider the discrete-time Cox-Ross-Rubinstein model with \(N+1\) time instants \(t=0,1, \ldots, N\), with a riskless asset whose price \(A_{t}\) evolves as \(A_{t}=A_{0}(1+r)^{t}\), \(t=0,1, \ldots, N\). The evolution of \(S_{t-1}\) to \(S_{t}\) is given by
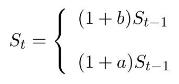
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Stochastic Finance With Market Examples
ISBN: 9781032288277
2nd Edition
Authors: Nicolas Privault
Question Posted: