We consider a riskless asset valued \(S_{k}^{(0)}=S_{0}^{(0)}, k=0,1, \ldots, N\), where the risk-free interest rate is \(r=0\), and a risky asset \(S^{(1)}\) whose returns \(R_{k}:=\frac{S_{k}^{(1)}-S_{k-1}^{(1)}}{S_{k-1}^{(1)}}\), \(k=1,2, \ldots, N\), form a sequence of independent identically distributed random variables taking three values \(\{-b

\[

p^{*}:=\mathbb{P}^{*}\left(R_{k}=bight)>0, \quad \theta^{*}:=\mathbb{P}^{*}\left(R_{k}=0ight)>0, \quad q^{*}:=\mathbb{P}^{*}\left(R_{k}=-bight)>0

\]

\(k=1,2, \ldots, N\). The information known to the market up to time \(k\) is denoted by \(\mathcal{F}_{k}\).

a) Determine all possible risk-neutral probability measures \(\mathbb{P}^{*}\) equivalent to \(\mathbb{P}\) in terms of the parameter \(\theta^{*} \in(0,1)\).

b) Assume that the conditional variance

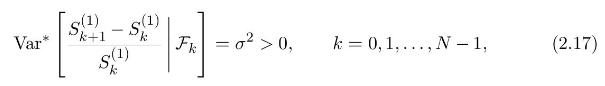
of the asset return is constant and equal to \(\sigma^{2}\). Show that this condition defines a unique risk-neutral probability measure \(\mathbb{P}_{\sigma}^{*}\) under a certain condition on \(b\) and \(\sigma\), and determine \(\mathbb{P}_{\sigma}^{*}\) explicitly.

Transcribed Image Text:

Var* s()-S() k+1 S() k Fk = 0 > 0, k = 0, 1,. ... N-1, (2.17)