An overhead crane is modeled as a two degree-of-freedom system as shown in Figure P6.14. The crane is modeled as a mass of \(1000 \mathrm{~kg}\) on a steel \((E=200 \times\) \(10^{9} \mathrm{~N} / \mathrm{m}^{2}\) ) fixed-fixed beam with a moment of inertia of \(4.2 \times 10^{-3} \mathrm{~m}^{4}\) and length of \(12 \mathrm{~m}\). The crane has an elastic steel rope of diameter \(20 \mathrm{~cm}\). At a specific instant, the length of the rope is \(10 \mathrm{~m}\) and is carrying a \(300 \mathrm{~kg}\) load. What are the two natural frequencies of the system?

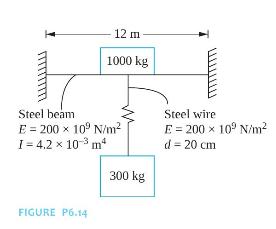
12 m 1000 kg Steel beam. Steel wire E 200 x 109 N/m E 200 x 109 N/m I = 4.2 10 3 m4 d = 20 cm 300 kg FIGURE P6.14