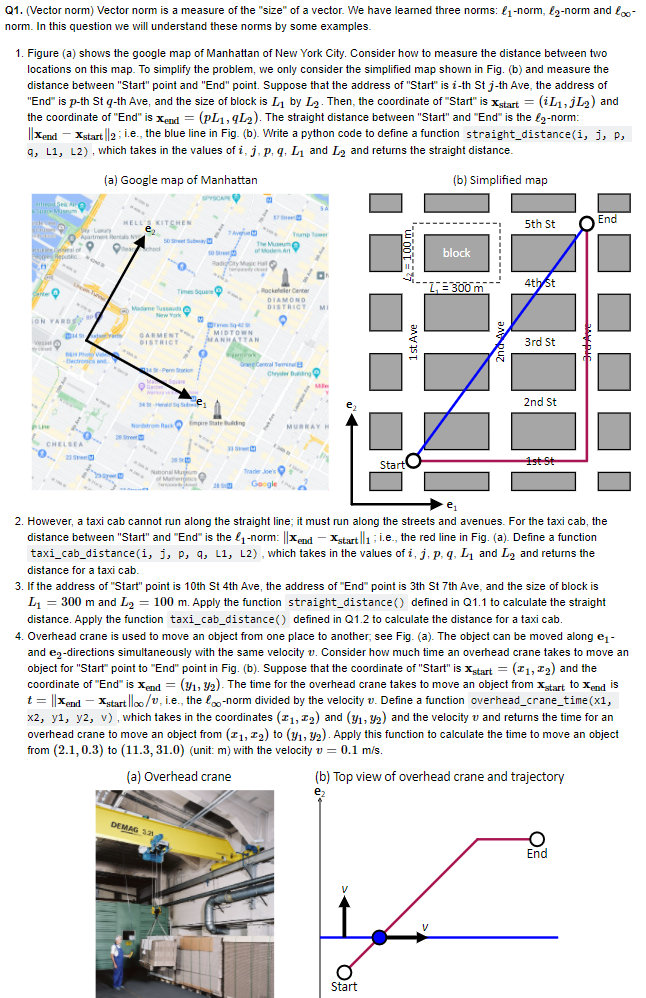
(Vector norm) Vector norm is a measure of the "size" of a vector. We have learned three norms: 11-norm, 22-norm and -norm. In this question we will understand these norms by some examples.

1. Figure (a) shows the google map of Manhattan of New York City. Consider how to measure the distance between two locations on this map. To simplify the problem, we only consider the simplified map shown in Fig. (b) and measure the distance between "Start" point and "End" point. Suppose that the address of "Start" is ii-th St jj-th Ave, the address of "End" is pp-th St qq-th Ave, and the size of block is L1L1 by L2L2. Then, the coordinate of "Start" is xstart=(iL1,jL2)xstart=(iL1,jL2) and the coordinate of "End" is xend=(pL1,qL2)xend=(pL1,qL2). The straight distance between "Start" and "End" is the 22-norm: xendxstart2xendxstart2; i.e., the blue line in Fig. (b). Write a python code to define a function straight_distance(i, j, p, q, L1, L2), which takes in the values of ii, jj, pp, qq, L1L1 and L2L2 and returns the straight distance.
2. However, a taxi cab cannot run along the straight line; it must run along the streets and avenues. For the taxi cab, the distance between "Start" and "End" is the 11-norm: xendxstart1xendxstart1; i.e., the red line in Fig. (a). Define a function taxi_cab_distance(i, j, p, q, L1, L2), which takes in the values of ii, jj, pp, qq, L1L1 and L2L2 and returns the distance for a taxi cab.
3. If the address of "Start" point is 10th St 4th Ave, the address of "End" point is 3th St 7th Ave, and the size of block is L1=300L1=300 m and L2=100L2=100 m. Apply the function straight_distance() defined in Q1.1 to calculate the straight distance. Apply the function taxi_cab_distance() defined in Q1.2 to calculate the distance for a taxi cab.
4. Overhead crane is used to move an object from one place to another; see Fig. (a). The object can be moved along e1e1- and e2e2-directions simultaneously with the same velocity vv. Consider how much time an overhead crane takes to move an object for "Start" point to "End" point in Fig. (b). Suppose that the coordinate of "Start" is xstart=(x1,x2)xstart=(x1,x2) and the coordinate of "End" is xend=(y1,y2)xend=(y1,y2). The time for the overhead crane takes to move an object from xstartxstart to xendxend is t=xendxstart/vt=xendxstart/v, i.e., the -norm divided by the velocity vv. Define a function overhead_crane_time(x1, x2, y1, y2, v), which takes in the coordinates (x1,x2)(x1,x2) and (y1,y2)(y1,y2) and the velocity vv and returns the time for an overhead crane to move an object from (x1,x2)(x1,x2) to (y1,y2)(y1,y2). Apply this function to calculate the time to move an object from (2.1,0.3)(2.1,0.3) to (11.3,31.0)(11.3,31.0) (unit: m) with the velocity v=0.1v=0.1 m/s.

Q1. (Vector norm) Vector norm is a measure of the "size" of a vector. We have learned three norms: li-norm, 1g-norm and leo- norm. In this question we will understand these norms by some examples. 1. Figure (a) shows the google map of Manhattan of New York City. Consider how to measure the distance between two locations on this map. To simplify the problem, we only consider the simplified map shown in Fig. (b) and measure the distance between "Start" point and "End" point. Suppose that the address of "Start" is i-th St j-th Ave, the address of "End" is p-th St q-th Ave, and the size of block is L1 by L2. Then, the coordinate of "Start" is Xstart = (iL1, L2) and the coordinate of "End" is Xend = (PL1, L2). The straight distance between "Start" and "End" is the 12-norm: Xend Xstart ||2 ; i.e., the blue line in Fig. (b). Write a python code to define a function straight_distance(i, j, P, 9, L1, L2), which takes in the values of i, j, p, q, L1 and L2 and returns the straight distance. (a) Google map of Manhattan (b) Simplified map b inte End HELL'S KITCHEN ON 5th St The block Radio LE300 m 4th St Roller Center DIAMOND DISTRICT MI TON VAROR DUS Ves GARMENT DISTRICT MIDTOWN MANHATTAN 3rd St Gram Chrysler e 2nd St e MURRAY Stre CHELSEA Start Nation Me Trader Joe's Google e 2. However, a taxi cab cannot run along the straight line; it must run along the streets and avenues. For the taxi cab, the distance between "Start" and "End" is the ly-norm: || Xend Xstart || ; i.e., the red line in Fig. (a). Define a function taxi_cab_distance(i, j, P, 9, L1, L2), which takes in the values of i, j, p, q, L1 and L2 and returns the distance for a taxi cab. 3. If the address of "Start" point is 10th St 4th Ave, the address of "End" point is 3th St 7th Ave, and the size of block is L1 = 300 m and L2 = 100 m. Apply the function straight_distance() defined in Q1.1 to calculate the straight distance. Apply the function taxi_cab_distance() defined in Q1.2 to calculate the distance for a taxi cab. 4. Overhead crane is used to move an object from one place to another, see Fig. (a). The object can be moved along e- and ez-directions simultaneously with the same velocity v. Consider how much time an overhead crane takes to move an object for "Start" point to "End" point in Fig. (b). Suppose that the coordinate of "Start" is Xstart = (11, 12) and the coordinate of "End" is Xend = (y1, y2). The time for the overhead crane takes to move an object from start to Xend is t = || Xend Xstart ||0o/v, i.e., the log-norm divided by the velocity v. Define a function overhead_crane_time(x1, x2, yi, y2, v), which takes in the coordinates (11, 12) and (y1, y2) and the velocity v and returns the time for an overhead crane to move an object from (21, 22) to (91, 92). Apply this function to calculate the time to move an object from (2.1,0.3) to (11.3, 31.0) (unit: m) with the velocity v = 0.1 m/s (a) Overhead crane (b) Top view of overhead crane and trajectory e2 DEMAG 32 End Start Q1. (Vector norm) Vector norm is a measure of the "size" of a vector. We have learned three norms: li-norm, 1g-norm and leo- norm. In this question we will understand these norms by some examples. 1. Figure (a) shows the google map of Manhattan of New York City. Consider how to measure the distance between two locations on this map. To simplify the problem, we only consider the simplified map shown in Fig. (b) and measure the distance between "Start" point and "End" point. Suppose that the address of "Start" is i-th St j-th Ave, the address of "End" is p-th St q-th Ave, and the size of block is L1 by L2. Then, the coordinate of "Start" is Xstart = (iL1, L2) and the coordinate of "End" is Xend = (PL1, L2). The straight distance between "Start" and "End" is the 12-norm: Xend Xstart ||2 ; i.e., the blue line in Fig. (b). Write a python code to define a function straight_distance(i, j, P, 9, L1, L2), which takes in the values of i, j, p, q, L1 and L2 and returns the straight distance. (a) Google map of Manhattan (b) Simplified map b inte End HELL'S KITCHEN ON 5th St The block Radio LE300 m 4th St Roller Center DIAMOND DISTRICT MI TON VAROR DUS Ves GARMENT DISTRICT MIDTOWN MANHATTAN 3rd St Gram Chrysler e 2nd St e MURRAY Stre CHELSEA Start Nation Me Trader Joe's Google e 2. However, a taxi cab cannot run along the straight line; it must run along the streets and avenues. For the taxi cab, the distance between "Start" and "End" is the ly-norm: || Xend Xstart || ; i.e., the red line in Fig. (a). Define a function taxi_cab_distance(i, j, P, 9, L1, L2), which takes in the values of i, j, p, q, L1 and L2 and returns the distance for a taxi cab. 3. If the address of "Start" point is 10th St 4th Ave, the address of "End" point is 3th St 7th Ave, and the size of block is L1 = 300 m and L2 = 100 m. Apply the function straight_distance() defined in Q1.1 to calculate the straight distance. Apply the function taxi_cab_distance() defined in Q1.2 to calculate the distance for a taxi cab. 4. Overhead crane is used to move an object from one place to another, see Fig. (a). The object can be moved along e- and ez-directions simultaneously with the same velocity v. Consider how much time an overhead crane takes to move an object for "Start" point to "End" point in Fig. (b). Suppose that the coordinate of "Start" is Xstart = (11, 12) and the coordinate of "End" is Xend = (y1, y2). The time for the overhead crane takes to move an object from start to Xend is t = || Xend Xstart ||0o/v, i.e., the log-norm divided by the velocity v. Define a function overhead_crane_time(x1, x2, yi, y2, v), which takes in the coordinates (11, 12) and (y1, y2) and the velocity v and returns the time for an overhead crane to move an object from (21, 22) to (91, 92). Apply this function to calculate the time to move an object from (2.1,0.3) to (11.3, 31.0) (unit: m) with the velocity v = 0.1 m/s (a) Overhead crane (b) Top view of overhead crane and trajectory e2 DEMAG 32 End Start