Determine the FRF for the system described in Problem 8 using Euler integration to calculate the time-domain displacement due to the impulsive input force. To increase the FRF frequency resolution, use a total simulation time of \(1 \mathrm{~s}\). Given the time-domain displacement and force vectors, use the MATLAB \({ }^{\mathbb{B}}\) function \(\mathrm{fft}\) to calculate the complex-valued force transform, \(\mathrm{F}\), and displacement transform, \(\mathrm{x}\). Plot the real and imaginary parts (in \(\mathrm{m} / \mathrm{N}\) ) of their ratio, \(\mathrm{X} / \mathrm{F}\), versus frequency (in \(\mathrm{Hz}\) ). Use axis limits of axis ([0 \(500-5 \mathrm{e}-6\) \(5 e-6])\) for the real plot and axis limits of axis ( \([0500-1 e-51 e-6])\) for the imaginary plot.

 Problem 8.

A single degree of freedom spring-mass-damper system which is initially at rest at its equilibrium position is excited by an impulsive force with a magnitude of \(250 \mathrm{~N}\) over a time interval of \(0.5 \mathrm{~ms}\); see Fig. P7.8. If the mass is \(3 \mathrm{~kg}\), the stiffness is \(3 \times 10^{6} \mathrm{~N} / \mathrm{m}\), and the viscous damping coefficient is \(120 \mathrm{~N}-\mathrm{s} / \mathrm{m}\), complete the following.

 

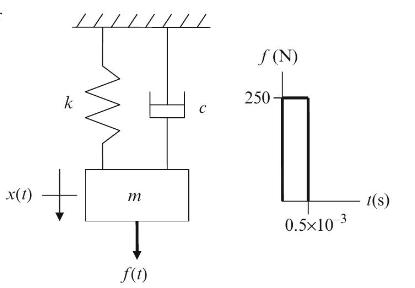
Fig. P7.8 Spring-mass-damper system excited by an impulsive force.

(a) Determine \(x(t)\) using Eq. 3.44. Plot the response (in \(\mu \mathrm{m}\) ) over a time period of \(0.3 \mathrm{~s}\) with a step size of \(1 \times 10^{-4} \mathrm{~s}\) in the time vector.
(b) Determine \(x(t)\) using Euler integration. Use a time step of \(1 \times 10^{-4} \mathrm{~s}\) and carry out your simulation for \(0.3 \mathrm{~s}\) ( 30,000 points). Plot \(x(t)\) (in \(\mu \mathrm{m}\) ) versus time.

Transcribed Image Text:

T C S(N) 250 x(t) m f(t) 0.5x10 3 1(s)