Figure P7 illustrates a robot arm that has two “links” connected by two “joints”—a shoulder or base joint and an elbow joint. There is a motor at each joint. The joint angles are θ₁ and θ₂. The (x, y) coordinates of the hand at the end of the arm are given by

 

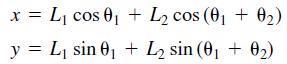
where L₁ and L₂ are the lengths of the links.

Polynomials are used for controlling the motion of robots. If we start the arm from rest with zero velocity and acceleration, the following polynomials are used to generate commands to be sent to the joint motor controllers

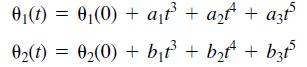
where θ₁(0) and θ₂(0) are the starting values at time t = 0. The angles θ₁(t_f) and θ₂(t_f) are the joint angles corresponding to the desired destination of the arm at time t_f. The values of θ₁(0), θ₂(0), θ₁(t_f), and θ₂(t_f) can be found from trigonometry, if the starting and ending (x, y) coordinates of the hand are specified.

a. Set up a matrix equation to be solved for the coefficients a₁, a₂, and a₃, given values for θ₁(0), - θ₁(t_f), and t_f. Obtain a similar equation for the coefficients b₁, b₂, and b₃.

b. Use MATLAB to solve for the polynomial coefficients given the values

t_f = 2 sec, θ₁(0) = -19°, θ₂(0) = 44°, θ₁(t_f) = 43°, and θ₂(t_f) = 151..

(These values correspond to a starting hand location of x = 6.5, y = 0 ft and a destination location of x = 0, y = 2 ft for L₁ = 4 and L₂ = 3 ft.)

c. Use the results of part b to plot the path of the hand.

Transcribed Image Text:

x = L, cos 0, + L2 cos (01 + 02) y = L, sin 01 + L2 sin (01 + 02)