For the two degree of freedom spring-mass-damper system shown in Fig. P5.5, complete the following if \(k_{a}=2 \times 10^{5} \mathrm{~N} / \mathrm{m}, \quad k_{b}=5.5 \times 10^{4} \mathrm{~N} / \mathrm{m}\), \(c_{a}=60 \mathrm{~N}-\mathrm{s} / \mathrm{m}, c_{b}=16.5 \mathrm{~N}-\mathrm{s} / \mathrm{m}, m_{a}=2.5 \mathrm{~kg}\), and \(m_{b}=1.2 \mathrm{~kg}\).

(a) Obtain the equations of motion in matrix form and transform them into modal coordinates \(q_{1}\) and \(q_{2}\). Normalize your eigenvectors to the force location, coordinate \(x_{2}\). Verify that proportional damping exists.

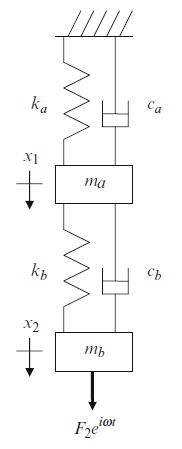
Fig. P5.5 Two degree of freedom spring-mass-damper system under forced vibration.

(b) Determine the FRFs \(Q_{1} / R_{1}, Q_{2} / R_{2}\), and \(X_{2} / F_{2}\). Express them in equation form and then plot the real and imaginary parts (in \(\mathrm{m} / \mathrm{N}\) ) versus frequency (in \(\mathrm{rad} / \mathrm{s})\). Use a frequency range of \(0: 0.1: 600 ;(\mathrm{rad} / \mathrm{s})\).

Transcribed Image Text:

ka Ca x1 ma kb x2 + mb icot F2e"