Reconsider the restroom door of Example 3.9. The man, instead of kicking the door, pushes it so
Question:
Reconsider the restroom door of Example 3.9. The man, instead of kicking the door, pushes it so that it opens to \(80^{\circ}\) and then lets go. How long will it take the door after he lets go to close to within \(5^{\circ}\) of being shut if it is designed
(a) with critical damping and
(b) with a damping ratio of 1.5 ?
Data From Example 3.9:
The restroom door of Figure 3.13 is equipped with a torsional spring and a torsional viscous damper so that it automatically returns to its closed position after being opened. The door has a mass of \(60 \mathrm{~kg}\) and a centroidal moment of inertia about an axis parallel to the axis of the door's rotation of \(7.2 \mathrm{~kg} \cdot \mathrm{m}^2\). The torsional spring has a stiffness of \(25 \mathrm{~N} \cdot \mathrm{m} / \mathrm{rad}\).
(a) What is the damping coefficient such that the system is critically damped?
(b) A man with an armload of packages, but in a hurry, kicks the door to cause it to open. What angular velocity must his kick impart to cause the door to open \(70^{\circ}\) ?
(c) How long after his kick will the door return to within \(5^{\circ}\) of completely closing?
(d) Repeat parts a through \(\mathrm{c}\) if the door is designed with a damping ratio, \(\zeta=1.3\).
Figure 3.13: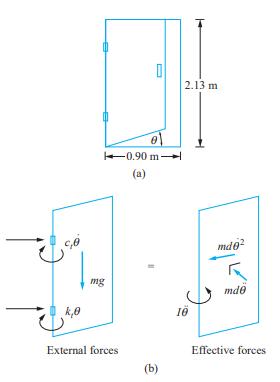
Step by Step Answer:






