The differential equation of motion for a cylinder rolling on a concave cylindrical surface is \(\ddot{\theta}+\frac{2}{3} \frac{g}{R-r} \theta=0\), where \(g\) is the gravitational constant.

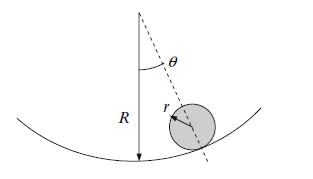
Fig. P2.3 Cylinder rolling on a concave cylindrical surface

(a) Write the expression for the natural frequency, \(\omega_{n}(\mathrm{rad} / \mathrm{s})\).

(b) If the free vibration is described as \(\theta(t)=A \sin \left(\omega_{n} t+\Phi_{s}\right)\), determine expressions for \(A\) and \(\Phi_{s}\) if the initial angle is \(\theta_{0}\) and the initial angular velocity is \(\dot{\theta}_{0}\).

(c) If \(R=200 \mathrm{~mm}, r=10 \mathrm{~mm}, \theta_{0}=5^{\circ}=0.087 \mathrm{rad}\), and \(\dot{\theta}_{0}=0\), plot \(\theta(t)\) (deg) using the function from part \(\mathrm{b}\) for the time interval from \(t=0\) to \(5 \mathrm{~s}\) in steps of \(0.005 \mathrm{~s}\).

Transcribed Image Text:

R