Consider the following two-person version of the language PUZZLE that was described in Problem 7.28. Each player starts with an ordered stack of puzzle cards. The players take turns placing the cards in order in the box and may choose which side faces up. Player I wins if all hole positions are blocked in the final stack, and Player II wins if some hole position remains unblocked. Show that the problem of determining which player has a winning strategy for a given starting configuration of the cards is PSPACE-complete.

Problem 7.28.

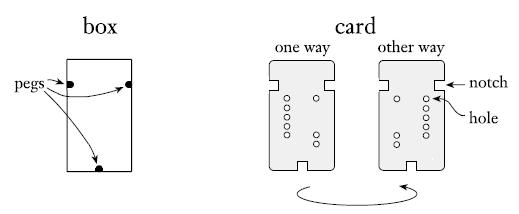
You are given a box and a collection of cards as indicated in the following figure. Because of the pegs in the box and the notches in the cards, each card will fit in the box in either of two ways. Each card contains two columns of holes, some of which may not be punched out. The puzzle is solved by placing all the cards in the box so as to completely cover the bottom of the box (i.e., every hole position is blocked by at least one card that has no hole there). Let PUZZLE = {〈c₁, . . . , c_k〉| each c_i represents a card and this collection of cards has a solution}. Show that PUZZLE is NP-complete.

Transcribed Image Text:

card other way box one way notch pegs hole 00000 00 0o 00000