Let AMBIG CFG = {G| G is an ambiguous CFG}. Show that AMBIGCFG is undecidable. Use a

Question:

Let AMBIG_CFG = {〈G〉| G is an ambiguous CFG}. Show that AMBIGCFG is undecidable. Use a reduction from PCP. Given an instance

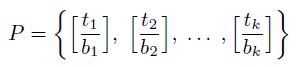
of the Post Correspondence Problem, construct a CFG G with the rules

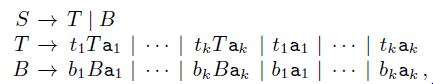
S - T|B T + tịTa1|| B - bị Bai | | tkTak | tia1 | | br Bak | biai | .. | tkak | bkak ,

where a₁, . . . , a_k are new terminal symbols. Prove that this reduction works.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Introduction to the theory of computation

ISBN: 978-0470530658

3rd edition

Authors: Michael Sipser

See More Books

Question Posted: Sep 02, 2020 04:49 AM

See More Questions

Prove that the following two languages are undecidable. a. OVERLAP CFG = {G,H| G and H are CFGs where L(G) L(H) }. Adapt the hint in Problem 5.21. b. PREFIX-FREE CFG = {G| G is a CFG where L(G) is...
Say that an NFA is ambiguous if it accepts some string along two different computation branches. Let AMBIG NFA = {N| N is an ambiguous NFA}. Show that AMBIGNFA is decidable. One elegant way to solve...
Let C = {G, x| G is a CFG x is a substring of some y L(G)}. Show that C is decidable. An elegant solution to this problem uses the decider for E CFG .
Paige buys a tool shed priced at $5990, but pays $6289.50 with tax. What is the tax rate where Paige lives?
Consider the following data on mating in birds. Do matings deviate from independence, and what might it mean? Test the above table for independence. Blue Male Green Male Red female Blue female Green...
How do the different types of memory interact in our everyday experience? (159)
Understand exporting as a foreign market entry strategy. 1239
During the next four months, a customer requires, respectively, 500, 650, 1000, and 700 units of a commodity, and no backlogging is allowed (that is, the customers requirements must be met on time)....
Troy Engines, Ltd., manufactures a variety of engines for use in heavy equipment. The company has always produced all of the necessary parts for its engines, including all of the carburetors. An...
a. i. On analysis a hydrocarbon was found to contain 0.72 g of carbon and 0.18 g of hydrogen. What is the empirical formula of the hydrocarbon? ii. Further investigation showed that the relative...
Prove that there exists an undecidable subset of {1} * .
Show that A is Turing-recognizable iff A m A TM .
Consider the many possible distributions of grades on a quiz in a statistics class; imagine that the grades could range from 0 to 100. For each of the following situations, give a hypothetical mean...
Sunland Corp. exchanged Building 24, which has an appraised value of $1,815,000, a cost of $2,842,000, and accumulated depreciation of $1,272,000, for Building M which belongs to Oriole Ltd. Building...
Conlon Chemicals manufactures paint thinner. Information on the work in process follows: -Beginning Inventory, 43,000 partially complete gallons -Transferred out, 211300 gallons -Ending inventory...
Mr . Nikola Tesla launched Tesla Supermart on December 1 , 2 0 x 1 with a cash investment of 1 5 0 , 0 0 0 . The following are additional transactions for the month: 2 Equipment valued at 2 0 , 0...
The Robots: Stealing Our Jobs or Solving Labour Shortages? As the coronavirus pandemic enveloped the world, businesses increasingly turned to automation in order to address rapidly changing...
Aquazona Pool Company is a custom pool builder. The company recently completed a pool for the Drayna family ( Job 1 3 2 4 ) as summarized on the incomplete job cost sheet below. Assume the company...
Input a number (X) and create a program that allows the user to select finding the area (Area) of one of the following: The area of a square with side X, Area = X * X The area of a circle with...
Write a while loop that uses an explicit iterator to accomplish the same thing as Exercise 7.3. Exercise 7.3. Write a for-each loop that calls the addInterest method on each BankAccount object in a...
We need to upgrade a channel to a higher bandwidth. Answer the following questions: a. How is the rate improved if we double the bandwidth? b. How is the rate improved if we double the SNR?
What is the theoretical capacity of a channel in each of the following cases? a. Bandwidth: 20 KHz SNR dB = 40 b. Bandwidth: 200 KHz SNR dB = 4 c. Bandwidth: 1 MHz SNR dB = 20
If the peak voltage value of a signal is 20 times the peak voltage value of the noise, what is the SNR? What is the SNR dB ?
7 . 4 3 Buy - side vs . sell - side analysts' earnings forecasts. Refer to the Financial Analysts Journal ( July / August 2 0 0 8 ) study of earnings forecasts of buy - side and sell - side analysts,...
Bond P is a premium bond with a coupon of 8.6 percent , a YTM of 7.35 percent, and 15 years to maturity. Bond D is a discount bond with a coupon of 8.6 percent, a YTM of 10.35 percent, and also 15...
QUESTION 2 (25 MARKS) The draft financial statements of Sirius Bhd, Vega Bhd, Rigel Bhd and Capella for the year ended 31 December 2018 are as follows: Statement of Profit or Loss for the year ended...

Let AMBIG CFG = {G| G is an ambiguous CFG}. Show that AMBIGCFG is undecidable. Use a

Question:

S - T|B T + tịTa1|| B - bị Bai | | tkTak | tia1 | | br Bak | biai | .. | tkak | bkak ,

Step by Step Answer:

To Prove AMBIGCFG is undecidable Method Using Reduction from PCP Proof I If P has a match with t i1 ...View the full answer

Introduction to the theory of computation

Students also viewed these Computer science questions