A practical method for interpolating a set of points with a curve is to use cubic splines. We are given a set {(x_i, y_i) : i = 0, 1, . . . , n} of n + 1 point-value pairs, where x₀1 n. We wish to fit a piecewise-cubic curve (spline) f (x) to the points. That is, the curve f (x) is made up of n cubic polynomials f_i(x) = a_i + b_ix + c_ix² + d_ix³ for i = 0, 1, . . . , n − 1, where if x falls in the range x_i x x_i+1, then the value of the curve is given by f (x) = f_i(x − x_i). The points x_i at which the cubic polynomials are "pasted" together are called knots. For simplicity, we shall assume that x_i = i for i = 0, 1, . . . , n.

To ensure continuity of f (x), we require that

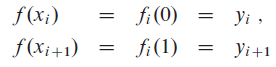
for i = 0, 1, . . . , n − 1. To ensure that f (x) is sufficiently smooth, we also insist that the first derivative be continuous at each knot.

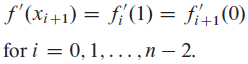
for i = 0, 1, . . . , n − 2.

a. Suppose that for i = 0, 1, . . . , n, we are given not only the point-value pairs {(x_i, y_i)} but also the first derivatives D_i = f' (x_i) at each knot. Express each coefficient a_i, b_i, c_i, and d_i in terms of the values y_i, y_i+1, D_i, and D_i+1. (Remember that x_i = i.) How quickly can we compute the 4n coefficients from the point-value pairs and first derivatives?

The question remains of how to choose the first derivatives of f (x) at the knots. One method is to require the second derivatives to be continuous at the knots.

for i = 0, 1, . . . , n − 2. At the first and last knots, we assume that f" (x₀) = f"₀ (0) = 0 and f" (x_n) = f"_n-1(1) = 0, these assumptions make f"(x) a natural cubic spline.

b. Use the continuity constraints on the second derivative to show that for i = 1, 2, . . . ,n − 1,

c. Show that

d. Rewrite equations (28.21)−(28.23) as a matrix equation involving the vector D = ⟨D₀, D₁, . . . ,D_n⟩ of unknowns. What attributes does the matrix in your equation have?

e. Argue that a natural cubic spline can interpolate a set of n + 1 point-value pairs in O(n) time.

f. Show how to determine a natural cubic spline that interpolates a set of n + 1 points (x_i, y_i) satisfying x₀ 1 i is not necessarily equal to i. What matrix equation must your method solve, and how quickly does your algorithm run?

f'(x;+1) = f{(1) = fi+1(0) for i = 0, 1, ...,n 2.