An alternative analysis of the running time of randomized quicksort focuses on the expected running time of each individual recursive call to RANDOMIZED-QUICKSORT, rather than on the number of comparisons performed.

a.?Argue that, given an array of size?n, the probability that any particular element is chosen as the pivot is?1/n. Use this to define indicator random variables?X_i = I {i th smallest element is chosen as the pivot}. What is E[X_i]?

b.?Let T (n) be a random variable denoting the running time of quicksort on an array of size n. Argue that

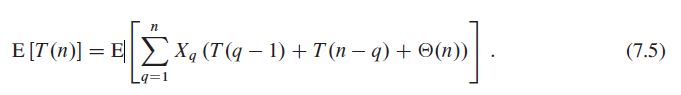
c.?Show that we can rewrite equation (7.5) as

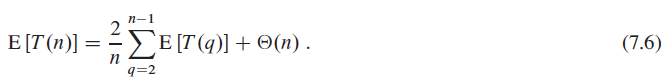
d.?Show that

Split the summation into two parts, one for k = 2,3, . . . , ?n/2? - 1 and one for k = ?n/2?, . . . ,n ? 1.

e.?Using the bound from equation (7.7), show that the recurrence in equation (7.6) has the solution E [T (n)] = ?(n lg n). Show, by substitution, that E[T (n)] ? an lg n for sufficiently large n and for some positive constant a.

Transcribed Image Text:

n-1 E[T (n)] = Σ Ε Τω) ETQ] + Θ(1). (7.6) п