Complementary slackness describes a relationship between the values of primal variables and dual constraints and between the values of dual variables and primal constraints. Let x? be a feasible solution to the primal linear program given in (29.16)-(29.18), and let y? be a feasible solution to the dual linear program given in (29.83)-(29.85). Complementary slackness states that the following conditions are necessary and sufficient for x? and y? to be optimal:

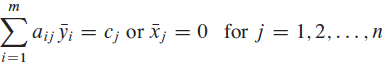
and

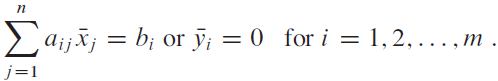
a.?Verify that complementary slackness holds for the linear program in lines (29.53)?(29.57).

b.?Prove that complementary slackness holds for any primal linear program and its corresponding dual.

c.?Prove that a feasible solution?x??to a primal linear program given in lines (29.16)?(29.18) is optimal if and only if there exist values?y??=?(y?₁, y?₂, . . . ,y?_m)?such that

1. y? is a feasible solution to the dual linear program given in (29.83)?(29.85),

2.?^m_?i=1?a_ij y? = c_j for all j such that x_j > 0, and

3.?y?_i = 0 for all i such that ?ⁿ_j-1 a_ij x_?ji.

Eaijx; = b; or ; = 0 for i = 1,2, ., m j=1