Let Q be a set of n points in the plane. We say that point (x, y) dominates point (x?, y?) if x ? x? and y ? y?. A point in Q that is dominated by no other points in Q is said to be maximal. That Q may contain many maximal points, which can be organized into maximal layers as follows. The first maximal layer L₁ is the set of maximal points of Q. For i > 1, the i th maximal layer Li is the set of maximal points in

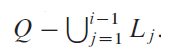
Suppose that Q has k nonempty maximal layers, and let y_i be the y-coordinate of the leftmost point in L_i for i = 1, 2, . . . ,k. For now, assume that no two points in Q have the same x- or y-coordinate.

a.?Show that?y₁ > y₂ > .... > y_k.

Consider a point?(x, y)?that is to the left of any point in?Q?and for which?y?is distinct from the?y-coordinate of any point in?Q. Let?Q??=?Q???{(x, y)}.

b.?Let?j?be the minimum index such that?y_jk, in which case we let j = k + 1. Show that the maximal layers of Q? are as follows.?

If?j???k, then the maximal layers of?Q??are the same as the maximal layers of?Q, except that?L_j also includes (x, y) as its new leftmost point.

If?j?=?k?+?1, then the first?k?maximal layers of?Q??are the same as for?Q, but in addition,?Q??has a nonempty?(k?+?1)st maximal layer.?L_k+1 = {(x, y)}.

c. Describe an O(n lg n)-time algorithm to compute the maximal layers of a set Q of n points.?

d. Do any difficulties arise if we now allow input points to have the same x- or y-coordinate? Suggest a way to resolve such problems.

Transcribed Image Text:

Q -U L;. j=1