This problem develops properties of the Fibonacci numbers, which are defined by recurrence (3.22). We shall use the technique of generating functions to solve the Fibonacci recurrence. Define the generating function (or formal power series). F as

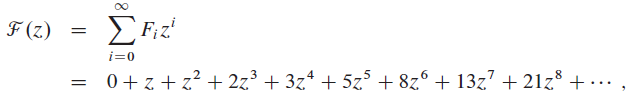
where Fi is the i th Fibonacci number.

a. Show that?

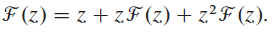
b. Show that

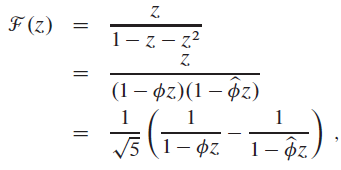
Where

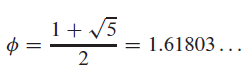
And

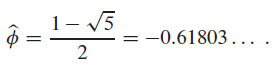
c. Show that

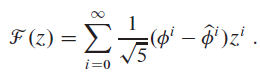
d. Use part (c) to prove that F_i = ?ⁱ /?5 for i > 0, rounded to the nearest integer. Observe that |??|

(3.22)

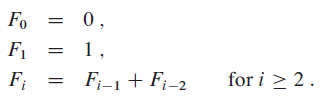
F (z) = z + zF (z) + zF (z).