Let b n denote the number of different binary trees with?n?nodes. In this problem, you will find
Question:
Let bn denote the number of different binary trees with?n?nodes. In this problem, you will find a formula for?bn, as well as an asymptotic estimate.
a.?Show that?b0 =?1?and that, for?n???1,
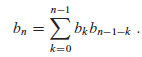
b. Referring to Problem 4-4 for the definition of a generating function, let B(x) be the generating function
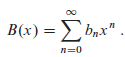
Show that B(x) = xB(x)2 +?1, and hence one way to express?B(x)?in closed form is
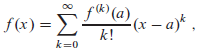
Where ? (k)(x) is the kth derivative of ? evaluated at x.
c. Show that

(the nth Catalan number) by using the Taylor expansion of ?1 - 4x around x = 0. (If you wish, instead of using the Taylor expansion, you may use the generalization of the binomial expansion (C.4) to nonintegral exponents n, where for any real number n and for any integer k, we interpret (nk)?to be?n(n???1) ??(n?-?k?+?1)/k!?if?k???0, and?0?otherwise.)
d. Show that
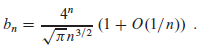
Step by Step Answer:

Introduction to Algorithms
ISBN: 978-0262033848
3rd edition
Authors: Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest





