A flow in which the velocity changes somewhere from subsonic (Ma < 1) to supersonic (Ma >
Question:
A flow in which the velocity changes somewhere from subsonic (Ma < 1) to supersonic (Ma > 1), or the reverse, is called transonic. Equation (12.5-9) shows that this cannot occur in a constant-diameter tube. The objective is to see what variation in cross-sectional area is needed to make transonic flows possible.
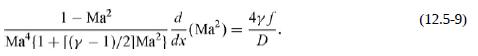
(a) Show that the continuity and inviscid momentum equations can be written as
(b) In isentropic (adiabatic and inviscid) flow the pressure and density gradients are related as in Eq. (P12.19-4). Show then that
This implies that v and S vary inversely for subsonic conditions, but in parallel for supersonic conditions. It indicates also that a finite acceleration can be sustained when Ma = 1 only if dS/dx = 0, thereby making both the numerator and denominator on the right-hand side zero. Thus, either a throat or bulge is necessary for adiabatic, inviscid flow to pass through Ma = 1.
(c) To prove that what is actually required for transonic flow is a throat, it is necessary to relate dv/dx to dMa/dx. Using conservation of energy for adiabatic flow [Eq. (12.5-7)] and evaluating the speed of sound as in Eq. (12.4-1), show that
where Γ = (γ − 1)/2. Substitution of this into Eq. (P12.20-3) gives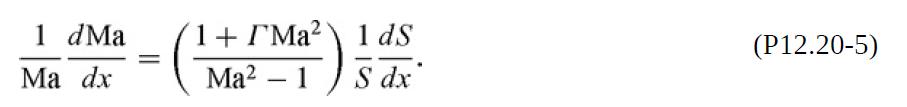
(d) Using l'Hôpital's rule, show that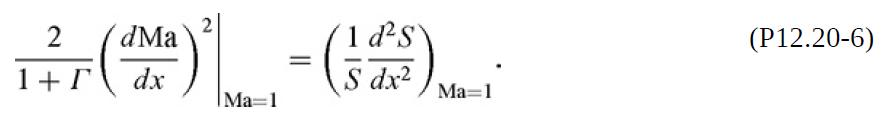
Thus, d2S/dx2 > 0 at Ma = 1, indicating that the gas velocity will pass through the speed of sound only where S is a minimum. Such a nozzle– diffuser combination, called a de Laval nozzle, is sketched in Fig. P12.20. Developed about 1890 for steam turbines by the Swedish engineer Gustaf de Laval (1845–1913), it is a standard part of modern rocket engines.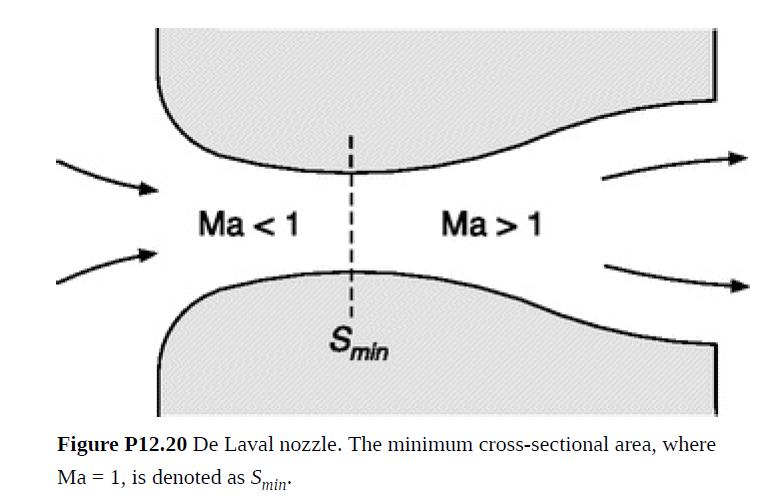

Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





