A manufacturer is planning to coat candy centers with thin films of chocolate. This is to be done by flowing molten chocolate onto a solid center by gravity, and then cooling quickly to solidify the film. A lubrication analysis of steady, gravity-driven flow of a thin film on a hemisphere is suggested as a way to explore the relationships among the process variables. Of particular interest are the thickness and uniformity of the coating. As shown in Fig. P8.4(a), a volume flow Q directed downward onto a hemisphere of radius a will create a liquid film of varying thickness, h(θ). It is expected that h ≪ a for most of the range of θ, so that within the film the solid surface will appear flat. This motivates using the local Cartesian coordinates in Fig. 8.4(b), which are related to the spherical ones as x = aθ and y = r − a. The thin-film assumption may be used throughout the analysis.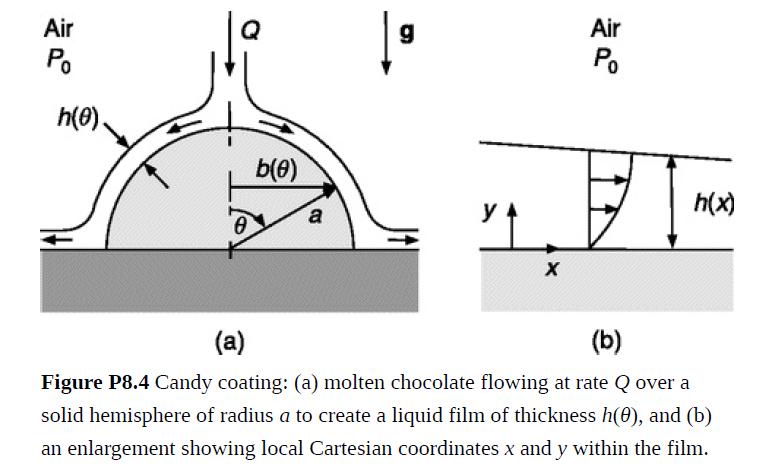(a) Neither h(θ) nor the mean velocity u(θ) is known in advance. Use a mass balance to relate these quantities to Q. (he radius b(θ) in Fig. 8.4(a) is helpful in this derivation.)

(b) Determine v_x(θ, y) and use it to find a second relationship between h(θ) and u(θ).

(c) Solve for h(θ) and u(θ). How is the film thickness predicted to vary with the operating parameters and with position?

Transcribed Image Text:

Air Po h(0). 0 b(e) a g X Air Po h(x) (a) (b) Figure P8.4 Candy coating: (a) molten chocolate flowing at rate Q over a solid hemisphere of radius a to create a liquid film of thickness h(0), and (b) an enlargement showing local Cartesian coordinates x and y within the film.