A uniform coating of liquid on a flat surface can be created by rapidly spinning the solid substrate after some liquid is applied. It is found that such films level quickly and then gradually become thinner. The thinning phase of the process is shown in Fig. P9.6. The film thickness at a given instant is uniform at h(t). Spinning the horizontal substrate at angular velocity ω causes the liquid to flow outward, slowly decreasing h. It is desired to predict h(t).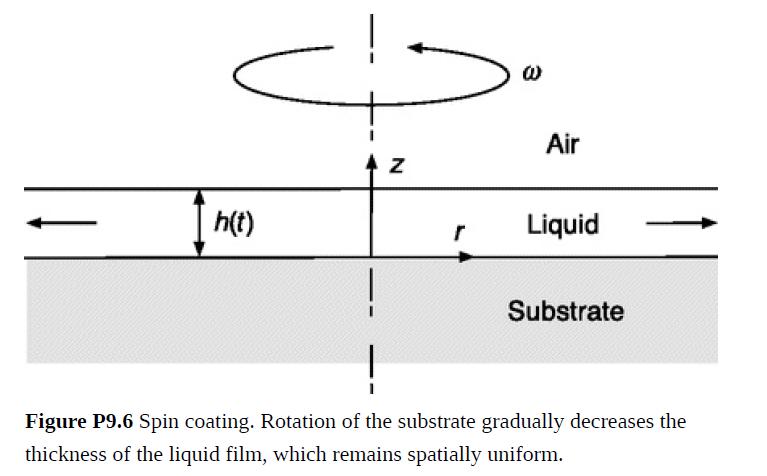

(a) Assume that v_θ(r) = ωr and that the r component of the Navier–Stokes equation can be simplified to

That is, suppose that the thinning is slow enough to be pseudosteady and that h is small enough to neglect the other viscous and inertial terms, as in a lubrication problem with Re = ωh²/ν ≪ 1. However, inertia is crucial here, in that the centrifugal force (ρv_θ²/r) is what causes the radial flow. Find v_r(r, z, t).

(b) Evaluate the radial flow rate per unit of circumference,

(c) Relate dh⁄dt to q. (Use a mass balance on a control volume that includes the liquid between r = 0 and an arbitrary radial position.)

(d) Solve for h(t), assuming that h(0) = h₀.

Transcribed Image Text:

h(t) ļ N r W Air Liquid Substrate Figure P9.6 Spin coating. Rotation of the substrate gradually decreases the thickness of the liquid film, which remains spatially uniform.