All of the liquid in a tank is to be transferred to another tank of the same size. As shown in Fig. P12.11, both are of radius R and at first they are slightly less than half full, with a liquid height H₀ in each. They are open at the top and are connected at the bottom by a pipe with a constant-speed centrifugal pump. The pump performs as in Eq. (12.3-6) with n = 2. For simplicity, assume that viscous losses outside the pump itself are negligible.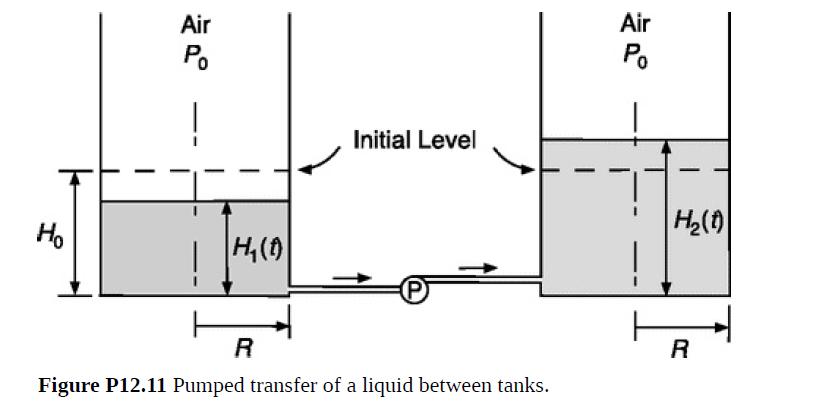

(a) What is the minimum value of the parameter A that is needed? In other words, how large must the pump be?

(b) Use the engineering Bernoulli equation and pump characteristics to show that

where ΔH = H₂ − H₁ is the difference in liquid levels. Combine this with a mass balance to obtain the differential equation that governs ΔH.

(c) A more convenient dependent variable than ΔH is ϕ = (A − ΔH)/H₀. Show that

where ϕ₀ = ϕ(0) = A/H₀ and V₀ = πR²H₀ is the initial liquid volume in either tank.

(d) What is the time t_p required to transfer the entire volume?

(e) How will Q vary with time?

Transcribed Image Text:

Ho Air Po -- H₁ (1) Initial Level R Figure P12.11 Pumped transfer of a liquid between tanks. Air Po H₂(1) R