An exact solution for the velocity in a conduit is usually obtainable only when each wall is a coordinate surface. An interesting exception is a duct with an equilateral triangular cross-section, as in Fig. P7.3. Adopting the coordinates in Bird et al. (2002, p. 106), the triangle side length is

and the duct length is L. Although the approach described below for finding v_z(x, y) seems as if it might be generalized to other polygons, unfortunately it works only for equilateral triangles and parallel plates.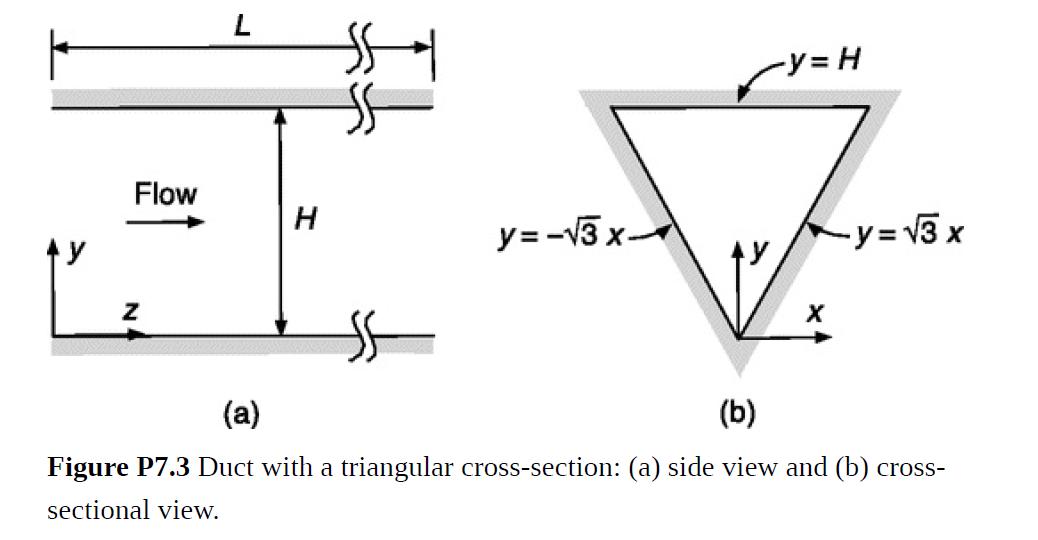

(a) Show that, as suggested in Landau and Lifshitz (1987, p. 54), a solution for the velocity may be constructed as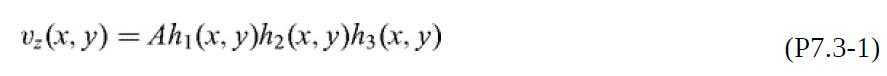

where A is a constant and h_i is the shortest distance of an interior point (x, y) to side i of the triangle. Find the functions h_i and then evaluate A in terms of the pressure drop.

(b) Relate the mean velocity U to the pressure drop.

(c) Show that the friction factor is given by fRe_H = 40/3.

Transcribed Image Text:

2H/√3