Consider fully developed flow at mean velocity U in a conduit with the elliptical cross-section in Fig. P7.4. The semi-axes are a and b and the length is L. The location of the wall is governed by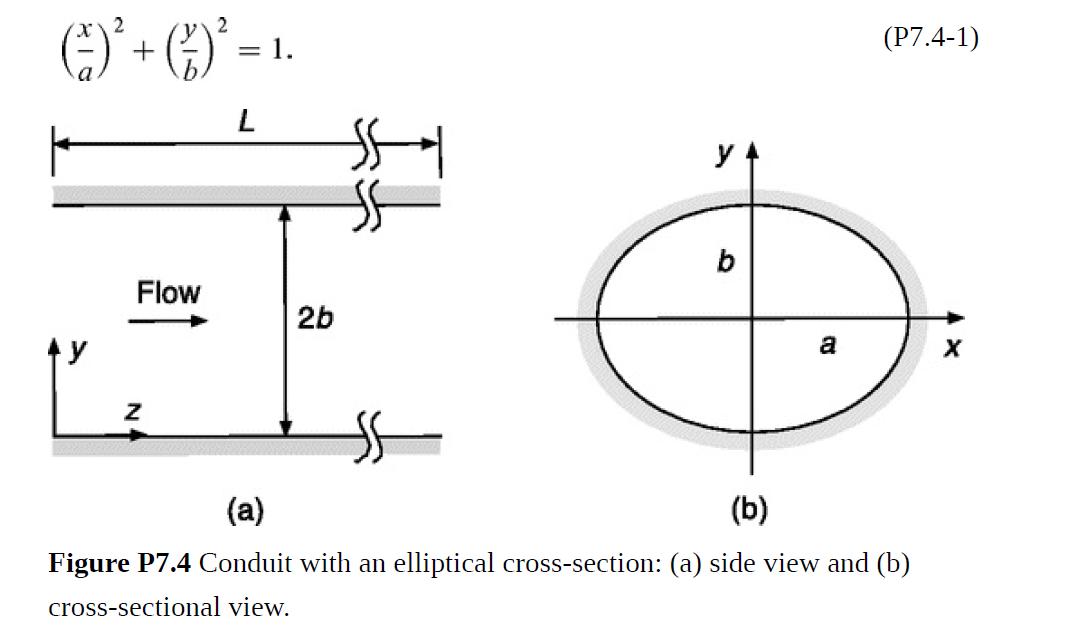

(a) The function

where A, B, and C are any constants, is a solution of the Navier–Stokes equation for fully developed flow in the z direction. Show that, as pointed out in Landau and Lifshitz (1987, p. 53), if A = −C/a² and B = −C/b² it will also satisfy the no-slip condition everywhere on the wall of the elliptical conduit.

(b) Complete the derivation of v_z(x, y) by using the Navier–Stokes equation to evaluate C in terms of the pressure drop.

(c) Show that U = C/2.

(d) The area of the ellipse is πab, but there is no exact, closed-form expression for its perimeter. A good approximation for the perimeter is

which reduces to the circumference of a circle when a = b. Show that the friction factor based on the hydraulic diameter is

as for a circular tube.

Transcribed Image Text:

(-)² + (²) ² Flow Z = 1. L 2b b a (P7.4-1) (a) (b) Figure P7.4 Conduit with an elliptical cross-section: (a) side view and (b) cross-sectional view.