As discussed in Section 2.5, at very high Re the friction factor in a tube becomes independent
Question:
As discussed in Section 2.5, at very high Re the friction factor in a tube becomes independent of Re and is affected only by the relative roughness of the wall. In this “fully rough” regime
where k is the effective roughness height and D is the tube diameter. Such an expression can be derived using two assumptions. One is to suppose that the mixing length near a rough wall is
In addition to the usual κ, there is now a dimensionless constant b that relates the length y0 to the roughness height k. Thus, the mixing length is postulated to increase as the wall becomes rougher. The second assumption is that τ0 is determined now not by viscous shear, but by pressure forces acting on the roughness elements that project in from the wall. This neglect of viscosity is consistent with the finding that f is independent of Re.
(a) Formulate the problem in terms of wall variables and show that
With viscous stresses neglected everywhere, including y = 0, this applies even at the wall.
(b) To obtain an expression for f, calculate the mean velocity as in Example 10.5-2. You may simplify the integration by assuming that y ≫ y0 over the entire cross-section. That is permissible because k ≪ D ordinarily and (as you will find) y0 < k.
(c) What value of b brings your result from part (b) into agreement with Eq. (P10.10-1)? An analogous model for flow past roughened flat plates has a best-fit value of b = 0.031 (Kays and Crawford, 1993, p. 231).


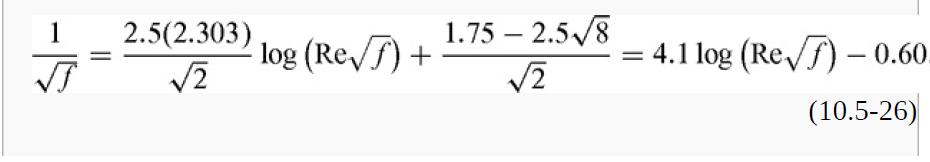

Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





