A weakness of both the power-law and logarithmic velocity profiles is that they give at y =
Question:
A weakness of both the power-law and logarithmic velocity profiles is that they give![]()
at y = R. Because symmetry requires that the shear stress vanish at the centerline, this implies that ε → 0 as y → R. The idea that turbulent eddies somehow disappear at the center of a tube is unrealistic and can create errors in heat and mass transfer calculations. A way around this problem was proposed by Reichardt (1951), who suggested that the eddy diffusivity outside the wall region be approximated as
where η = r⁄R, R+ is as defined in Eq. (10.2-6), and κ is an empirical constant.
(a) Show that the Reichardt eddy diffusivity leads to
where C is a constant.
(c) Where the law of the wall applies, η → 1. By choosing κ and C for consistency with Eq. (10.5-16), show that
Note that the right-hand side could be rewritten in terms of η alone, if desired, by using y+ = R+(1 − η).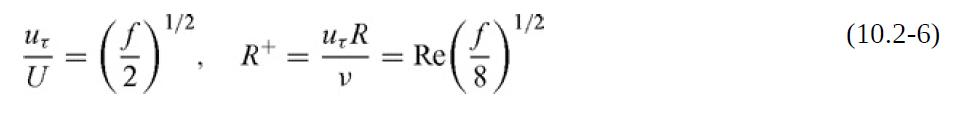

Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





