Rotating-disk electrodes are widely used to study electrochemical kinetics. As depicted in Fig. P9.12, a metal (e.g., platinum) electrode is embedded in the end of an insulating rod of radius R, which is immersed in an electrolyte solution. Rotating the rod at an angular velocity ω causes the nearby liquid to rotate, while also drawing it toward the end of the rod and throwing it outward. Thus, all three velocity components (v_r, v_θ, v_z) are nonzero. Because the flow helps deliver the reacting ions to the surface, a detailed knowledge of v is needed to interpret measured currents.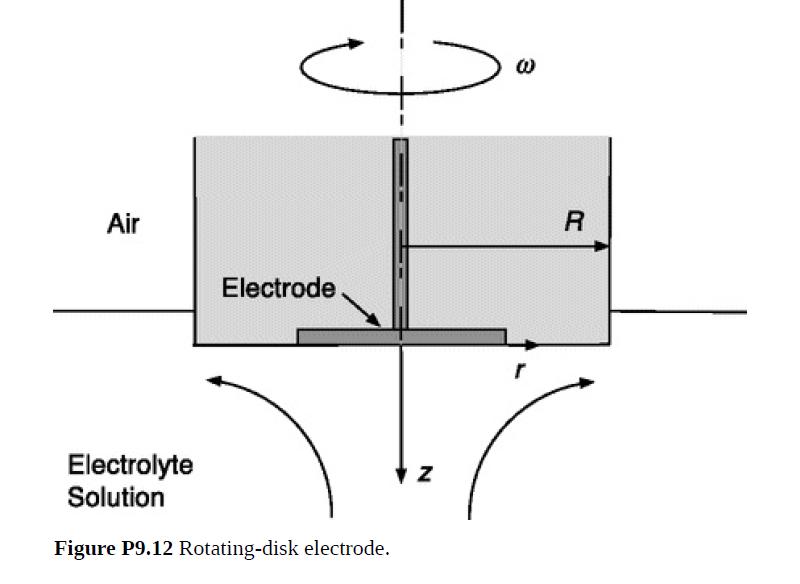

(a) In such systems the rod radius is large enough that the flow near the electrode is insensitive to R. If R is disregarded, show that the only way to make z dimensionless is

(b) Explain why the velocity might be assumed to be of the form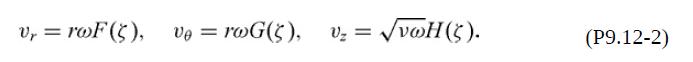

In particular, show that the continuity equation becomes

where the prime indicates differentiation with respect to ζ. Explain also why reasonable boundary conditions for the three unknown functions are

(c) Show that, if it is assumed also that the pressure is of the form

the Navier–Stokes equation becomes

Thus, the continuity equation and three-dimensional Navier–Stokes equation are reduced to a set of four ordinary differential equations. These coupled, nonlinear equations must be solved numerically.

(d) Although it does not influence the velocity near the electrode, R affects the torque that must be applied. Given that F′(0) = 0.5102 and G′(0) = – 0.6159 (Rogers and Lance, 1960), calculate the torque. You may assume that the immersion depth is small enough to enable you to neglect the shear stress on the side of the rod.

Transcribed Image Text:

Air Electrolyte Solution Electrode Figure P9.12 Rotating-disk electrode. Z @ R