Bubbles at large Re are typically shaped as spherical caps, as shown in Fig. P9.14. The trailing
Question:
Bubbles at large Re are typically shaped as spherical caps, as shown in Fig. P9.14. The trailing surface is more irregular than what is depicted, but the leading surface is almost a perfect spherical section. It is desired to predict the terminal velocity U for a bubble of density ρo and cap radius R that is rising in a liquid of density ρ. There are boundary layers on both the liquid and gas sides of the spherical surface. Surface tension is negligible in such large bubbles.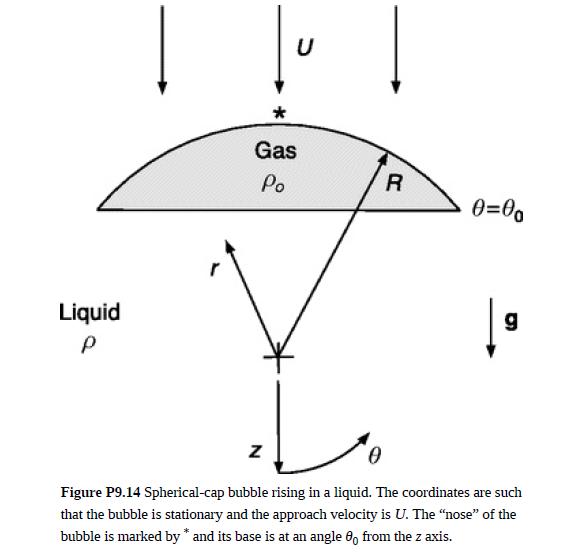
(a) Assume that on the liquid side of the top surface ℘ is that for potential flow past a complete sphere, as given in Eq. (P9.1-2). Convert ℘ to P to show that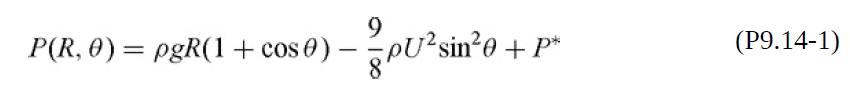
where P* is the pressure at the “nose” (θ = π).
(b) Even with a large tangential velocity at the top surface, most of the gas will circulate slowly. Thus, for the boundary layer on the gas side, the pressure will be nearly that in a static gas. Show that, in the gas,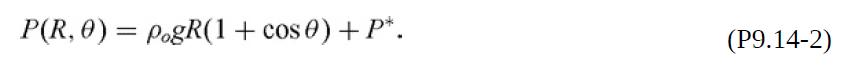
(c) If the surface tension and normal viscous stresses are both negligible, in principle we could simply equate the pressures from parts (a) and (b) and solve for U. However, show that this gives
which cannot be satisfied for all θ on the top surface.
(d) Less ambitious is to expect the approximate pressures to match only near the nose. By expanding the trigonometric functions about θ = π, show that this leads to
as in Davies and Taylor (1950).
(e) The Davies–Taylor equation is remarkably accurate for Re > 40 (Clift et al., 1978, p. 206), where Re is based on the liquid properties and the diameter of a sphere of equivalent volume (DE). For Re > 150, θ0≅130° and DE/R = 0.77. Calculate U for an air bubble in water with R = 1.0 cm.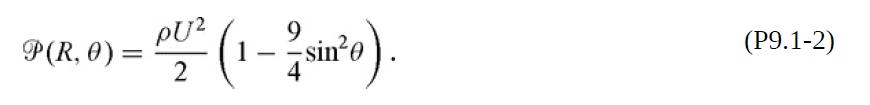
Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





