Suppose that a vapor condenses at a constant rate on a cold vertical wall, as shown in Fig. P5.3. As the liquid runs down the wall, the film thickness δ(x) and mean velocity u(x) both increase. Assume that the condensation begins at x = 0, such that u(0) = 0 = δ(0). The increase in volume flow from position x to x + Δx is v_cW Δx, where the condensation velocity v_c is given and W is the width of the wall.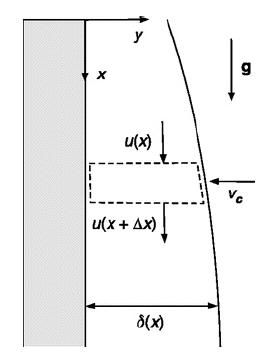

(a) Use a shell balance to relate δ(x) and u(x) to vc.

(b) If dδ⁄dx ≪ 1, it is found using the methods in Section 8.2 that the downward velocity is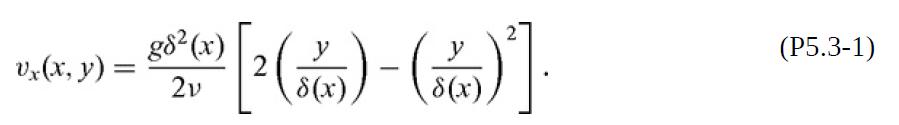

Use this and the result from part (a) to find u(x) and δ(x).

(c) Determine vy(x, y).

Transcribed Image Text:

1 X y u(x) u(x + AX) 8(x) jo g